今回は、機械学習モデルのハイパーパラメータをチューニングするのに用いられる Python のフレームワークの一つとして Hyperopt を使ってみる。 このフレームワークは、機械学習コンペティションの一つである Kaggle でよく用いられるものとして知られている。
なお、このブログでは過去にハイパーパラメータのチューニングについて Bayesian Optimization や Optuna を使った例を扱ったことがある。
今回使った環境は次の通り。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.14.2 BuildVersion: 18C54 $ python -V Python 3.7.2
下準備
まずは下準備として、必要になるパッケージをインストールする。
$ pip install hyperopt matplotlib scikit-learn pandas
単純な例で動作を確認する
機械学習モデルのハイパーパラメータを扱う前に、まずはもっと単純な例から始める。
手始めに、次のような一つの変数 x を取る関数の最大値を探す問題について考えてみよう。
グラフを見ると、最大値は 2 付近にあるようだ。

上記の関数の最大値を Hyperopt で探すサンプルコードは次の通り。
Hyperopt では、最適化したい目的関数を用意して、それを hyperopt.fmin() に渡す。
以下のサンプルコードにおいて目的関数は objective() という名前で定義している。
チューニングするパラメータは、どんな分布でどういった値域を持つのかあらかじめ定義しておく。
以下では hp.uniform('x', -5, +15) がそれで、値域が -5 ~ +15 の一様分布を定義している。
#!/usr/bin/env python # -*- coding: utf-8 -*- import math from hyperopt import hp from hyperopt import fmin from hyperopt import tpe def f(x): """最大値を見つけたい関数""" return math.exp(-(x - 2) ** 2) + math.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1) def objective(args): """最小化したい目的関数""" return -1 * f(args) # 元のタスクが最大化なので符号を反転する def main(): # 変数の値域を定義する space = hp.uniform('x', -5, +15) # 目的関数を最小化するパラメータを探索する best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100) # 結果を出力する print(best) if __name__ == '__main__': main()
上記に適当な名前をつけて実行する。 すると、たしかに解析的に確認していた最大値として 2 前後の値が得られる。
$ python hellohp.py
{'x': 2.0069551331288276}
探索過程を記録する
先ほどの例では、最終的に最適化された値が得られておしまいだった。
とはいえ、実際に使う場面では、その値がどういった経緯を経て得られたのか重要になる場合もある。
そこで、Hyperopt では Trials というオブジェクトに過程を記録できる。
次のサンプルコードでは Trials のインスタンスに探索過程を記録した上で、最後にそれを出力している。
#!/usr/bin/env python # -*- coding: utf-8 -*- import math from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import STATUS_OK def f(x): """最大値を見つけたい関数""" return math.exp(-(x - 2) ** 2) + math.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1) def objective(args): """最小化したい目的関数""" # 計算過程を追跡するときは目的関数の返り値を辞書にする return { 'loss': -1 * f(args), # 最小化する損失 (必須パラメータ) 'status': STATUS_OK, # 計算結果 (必須パラメータ) } def main(): # 変数の値域を定義する space = hp.uniform('x', -5, +15) # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 探索過程を出力する for item in trials.trials: vals = item['misc']['vals'] result = item['result'] print('vals:', vals, 'result:', result) if __name__ == '__main__': main()
実行すると、どのような値を探索して結果がどうだったのかが確認できる。
$ python trials.py
vals: {'x': [10.496518222653432]} result: {'loss': -0.14140262193324998, 'status': 'ok'}
vals: {'x': [13.094879827038248]} result: {'loss': -0.012312365591358516, 'status': 'ok'}
vals: {'x': [-2.0228004674552014]} result: {'loss': -0.19799926655007422, 'status': 'ok'}
...(snip)...
vals: {'x': [2.6501743089141496]} result: {'loss': -1.1054773169025645, 'status': 'ok'}
vals: {'x': [9.247128914308604]} result: {'loss': -0.35996620277329294, 'status': 'ok'}
vals: {'x': [7.18849940727293]} result: {'loss': -0.8872540482414317, 'status': 'ok'}
探索過程に色々な値を記録する
先ほど使った Trials オブジェクトには、実は自分で色々な値を記録することもできる。
次のサンプルコードでは、探索した時刻と関数の引数を記録している。
#!/usr/bin/env python # -*- coding: utf-8 -*- import time import math from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import STATUS_OK def f(x): """最大値を見つけたい関数""" return math.exp(-(x - 2) ** 2) + math.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1) def objective(args): """最小化したい目的関数""" return { 'loss': -1 * f(args), # 最小化する損失 (必須パラメータ) 'status': STATUS_OK, # 計算結果 (必須パラメータ) # 一定の制約の元に自由に入れて良い 'estimate_time': time.time(), 'vals': args, } def main(): # 変数の値域を定義する space = hp.uniform('x', -5, +15) # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 探索過程を出力する for item in trials.trials: result = item['result'] print('result:', result) if __name__ == '__main__': main()
上記を実行すると、探索した時刻や引数が得られていることが分かる。
$ python params.py
result: {'loss': -0.339479707912701, 'status': 'ok', 'estimate_time': 1548600261.9176042, 'vals': -1.407873925928973}
result: {'loss': -0.682422018336043, 'status': 'ok', 'estimate_time': 1548600261.919095, 'vals': 8.012065634262315}
result: {'loss': -0.055263914137346264, 'status': 'ok', 'estimate_time': 1548600261.920187, 'vals': -4.135976583356424}
...(snip)...
result: {'loss': -1.1031356060488282, 'status': 'ok', 'estimate_time': 1548600262.10813, 'vals': 2.65344333175562}
result: {'loss': -0.27738481344650867, 'status': 'ok', 'estimate_time': 1548600262.111007, 'vals': -1.6261239199291966}
result: {'loss': -0.14645158143456388, 'status': 'ok', 'estimate_time': 1548600262.1134, 'vals': -2.4222183825698775}
探索過程を可視化してみる
先ほどの例では、どんな風に探索が進められているのかがいまいちイメージしにくかった。 そこで、どんな風に探索しているのかをグラフ上にプロットしてみた。
#!/usr/bin/env python # -*- coding: utf-8 -*- import time import math from matplotlib import pyplot as plt import numpy as np from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import STATUS_OK def f(x): """最大値を見つけたい関数""" return math.exp(-(x - 2) ** 2) + math.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1) def objective(args): """最小化したい目的関数""" return { 'loss': -1 * f(args), # 最小化する損失 (必須パラメータ) 'status': STATUS_OK, # 計算結果 (必須パラメータ) 'vals': args, } def main(): # 変数の値域を定義する space = hp.uniform('x', -5, +15) # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 検索過程をグラフで可視化してみる args = [result['vals'] for result in trials.results] values = [-result['loss'] for result in trials.results] # 元のグラフをプロットする X = [x for x in np.arange(-5, 15, 0.1)] y = [f(x) for x in X] plt.plot(X, y) # 探索した場所をプロットする plt.scatter(args, values) # グラフを描画する plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show() if __name__ == '__main__': main()
上記に適当な名前をつけて実行する。
$ python visualize.py
すると、次のようなグラフが得られる。
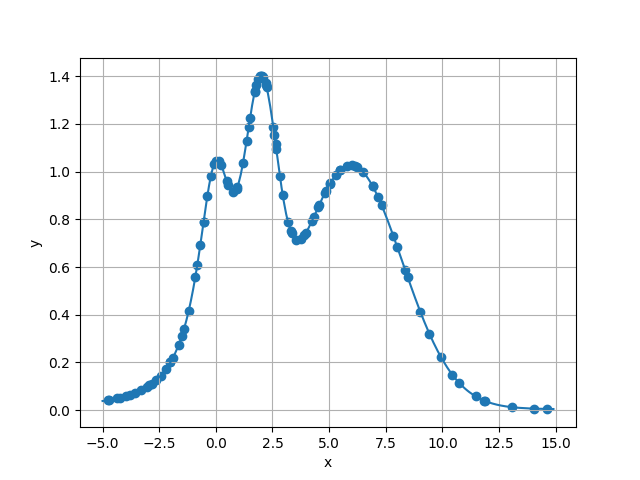
頂点付近以外にも、かなり色んな所を調べていることが伺える。
機械学習のモデルに適用してみる
続いては、ついに Hyperopt を機械学習のモデルに適用してみる。
モデルのアルゴリズムにはサポートベクターマシンを使った。
パラメータとしては kernel と C と gamma をチューニングする。
次のサンプルコードでは、目的関数でサポートベクターマシンを学習させて 5-Fold CV で Accuracy を評価している。
kernel は ['linear', 'rbf', 'poly'] の三種類から選ぶ。
C と gamma は常用対数で 0 ~ 100 と -10 ~ 1 の範囲で探索する。
2.303 を乗じているのは二進対数と常用対数に変換するため。
#!/usr/bin/env python # -*- coding: utf-8 -*- from functools import partial from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import space_eval from sklearn import datasets from sklearn.model_selection import StratifiedKFold from sklearn.model_selection import cross_validate from sklearn.svm import SVC def objective(X, y, args): """最小化したい目的関数""" # モデルのアルゴリズムに SVM を使う model = SVC(**args) # Stratified 5 Fold Cross Validation kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) scores = cross_validate(model, X=X, y=y, cv=kf) # 最小化なので符号を反転する return -1 * scores['test_score'].mean() def main(): # データセットを読み込む dataset = datasets.load_iris() X, y = dataset.data, dataset.target # 目的関数にデータセットを部分適用する f = partial(objective, X, y) # 変数の値域を定義する space = { # 底が自然対数なので 2.303 をかけて常用対数に変換する 'C': hp.loguniform('C', 2.303 * 0, 2.303 * +2), 'gamma': hp.loguniform('gamma', 2.303 * -2, 2.303 * +1), 'kernel': hp.choice('kernel', ['linear', 'rbf', 'poly']), } # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する best = fmin(fn=f, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 結果を出力する print(space_eval(space, best)) if __name__ == '__main__': main()
実行すると、次のような結果が得られる。 値は似通ったものになるはずだけど、結果は毎回異なるはず。
$ python svm.py
{'C': 1.9877559946331484, 'gamma': 0.7522911704230325, 'kernel': 'linear'}
探索を可視化してみる
さきほどと同じように、どのような値を探索したのかグラフにプロットしてみよう。
次のサンプルコードでは、カーネルを linear に決め打ちした状態で、Hyperopt が探索した C と gamma を二次元でプロットしている。
標準化した Accuracy の高低は点の色で表現している。
#!/usr/bin/env python # -*- coding: utf-8 -*- from functools import partial from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import STATUS_OK from hyperopt import space_eval from sklearn import datasets from sklearn.model_selection import StratifiedKFold from sklearn.model_selection import cross_validate from sklearn.svm import SVC import numpy as np import pandas as pd from matplotlib import pyplot as plt from matplotlib import cm def objective(X, y, args): """最小化したい目的関数""" # モデルのアルゴリズムに Linear SVM を使う model = SVC(kernel='linear', **args) # Stratified 5 Fold Cross Validation kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) scores = cross_validate(model, X=X, y=y, cv=kf) # 最小化なので符号を反転する return { 'loss': -1 * scores['test_score'].mean(), 'status': STATUS_OK, 'vals': args, } def main(): # データセットを読み込む dataset = datasets.load_iris() X, y = dataset.data, dataset.target # 目的関数にデータセットを部分適用する f = partial(objective, X, y) # 変数の値域を定義する space = { 'C': hp.loguniform('C', 2.303 * 0, 2.303 * +2), 'gamma': hp.loguniform('gamma', 2.303 * -2, 2.303 * +1), } # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する best = fmin(fn=f, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 結果を出力する print('best parameters:', space_eval(space, best)) # 探索過程を可視化する xs = [result['vals']['C'] for result in trials.results] ys = [result['vals']['gamma'] for result in trials.results] zs = np.array([-1 * result['loss'] for result in trials.results]) s_zs = (zs - zs.min()) / (zs.max() - zs.min()) # 0 ~ 1 の範囲に正規化する # プロットする sc = plt.scatter(xs, ys, c=s_zs, s=20, zorder=10, cmap=cm.cool) plt.colorbar(sc) plt.xlabel('C') plt.xscale('log') plt.ylabel('gamma') plt.yscale('log') plt.grid() plt.show() print('-- accuracy summary --') print(pd.Series(np.array(zs).ravel()).describe()) if __name__ == '__main__': main()
上記を実行する。
$ python svmplot.py
best parameters: {'C': 2.3141971486483675, 'gamma': 0.014160000992695598}
-- accuracy summary --
count 100.000000
mean 0.975800
std 0.008350
min 0.960000
25% 0.966667
50% 0.980000
75% 0.980000
max 0.986667
dtype: float64
すると、次のようなグラフが得られる。
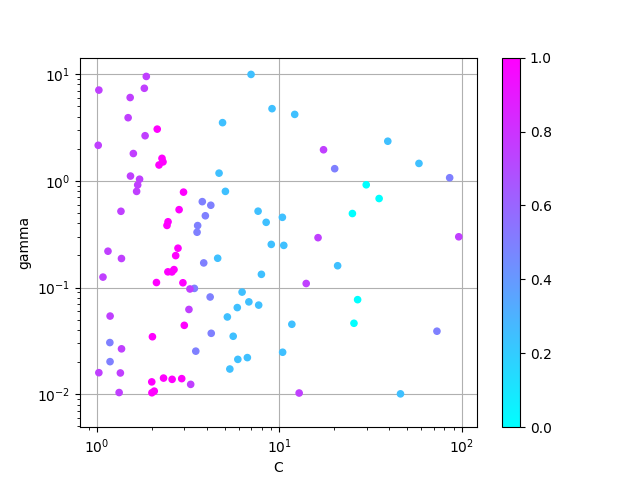
たしかに、場所によって性能に違いが出ているようだ。
見た感じ gamma よりも C の方が性能に違いを与えていそう。
複数のモデルから選ぶ
先ほどの例では、サポートベクターマシンの中でハイパーパラメータをチューニングしていた。 これだと、別のモデルを含めて評価したいときは別々に実行する必要がある。 そんなとき Hyperopt ではまとめて評価することもできる。
次のサンプルコードではランダムフォレスト、サポートベクターマシン、ロジスティック回帰を一度に評価している。
#!/usr/bin/env python # -*- coding: utf-8 -*- from functools import partial from hyperopt import hp from hyperopt import fmin from hyperopt import tpe from hyperopt import Trials from hyperopt import space_eval from hyperopt.pyll.base import scope from sklearn import datasets from sklearn.ensemble import RandomForestClassifier from sklearn.linear_model import LogisticRegression from sklearn.model_selection import StratifiedKFold from sklearn.model_selection import cross_validate from sklearn.svm import SVC def objective(X, y, args): """最小化したい目的関数""" classifiers = { 'svm': SVC, 'rf': RandomForestClassifier, 'logit': LogisticRegression, } classifier = classifiers.get(args['model_type']) del args['model_type'] model = classifier(**args) # Stratified 5 Fold Cross Validation kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) scores = cross_validate(model, X=X, y=y, cv=kf) # 最小化なので符号を反転する return -1 * scores['test_score'].mean() def main(): # データセットを読み込む dataset = datasets.load_iris() X, y = dataset.data, dataset.target # 目的関数にデータセットを部分適用する f = partial(objective, X, y) # 変数の値域を定義する space = hp.choice('algorithms', [ { 'model_type': 'rf', 'n_estimators': scope.int(hp.uniform('n_estimators', 1e+1, 1e+3)), 'max_depth': scope.int(hp.uniform('max_depth', 1e+1, 1e+3)), }, { 'model_type': 'svm', 'C': hp.uniform('C', 1e+0, 1e+2), 'gamma': hp.lognormal('gamma', 1e-2, 1e+1), }, { 'model_type': 'logit', 'solver': 'lbfgs', 'multi_class': 'auto', 'max_iter': 1000, } ]) # 探索過程を記録するオブジェクト trials = Trials() # 目的関数を最小化するパラメータを探索する best = fmin(fn=f, space=space, algo=tpe.suggest, max_evals=100, trials=trials) # 結果を出力する print(space_eval(space, best)) if __name__ == '__main__': main()
上記を実行してみよう。 このパラメータの中ではサポートベクターマシンが最も良い結果が得られたようだ。
$ python multimodel.py
{'C': 98.52420177369001, 'gamma': 0.011789334572006299, 'model_type': 'svm'}
いじょう。

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログ (1件) を見る