PyTorch に慣れるためにコードをたくさん読み書きしていきたい。 今回は MNIST データセットを使ってシンプルな AutoEncoder を書いてみる。
使った環境は次のとおり。
$ sw_vers ProductName: macOS ProductVersion: 14.5 BuildVersion: 23F79 $ python -V Python 3.11.9 $ sysctl machdep.cpu.brand_string machdep.cpu.brand_string: Apple M2 Pro $ pip list | egrep "(torch|matplotlib)" matplotlib 3.9.0 torch 2.3.1 torchvision 0.18.1
もくじ
下準備
下準備として必要なパッケージをインストールする。
$ pip install torch torchvision matplotlib
サンプルコード
早速だけど以下がサンプルコードになる。 説明は適宜、コメントの形で挿入している。
#!/usr/bin/env python3 import random import torch import torch.nn as nn import torch.optim as optim from matplotlib import pyplot as plt from torch.utils.data import DataLoader, random_split from torchvision import datasets, transforms def set_random_seed(seed): """シード値を設定する""" random.seed(seed) torch.manual_seed(seed) if torch.cuda.is_available(): torch.cuda.manual_seed_all(seed) def computing_device(force=None): """環境によって計算に使うデバイスを切り替える関数""" if force is not None: return force if torch.cuda.is_available(): return "cuda" if torch.backends.mps.is_available(): return "mps" return "cpu" class AutoEncoder(nn.Module): """ボトルネック部分で 32 次元まで圧縮する 3 層 AutoEncoder モデル""" def __init__(self): super(AutoEncoder, self).__init__() self.encoder = nn.Sequential( nn.Linear( in_features=28 * 28, out_features=128, ), nn.ReLU(inplace=True), nn.Linear( in_features=128, out_features=64, ), nn.ReLU(inplace=True), nn.Linear( in_features=64, out_features=32, ), ) self.decoder = nn.Sequential( nn.Linear( in_features=32, out_features=64, ), nn.ReLU(inplace=True), nn.Linear( in_features=64, out_features=128, ), nn.ReLU(inplace=True), nn.Linear( in_features=128, out_features=28 * 28, ), nn.Sigmoid(), ) def encode(self, x): """エンコードの処理をするメソッド""" return self.encoder(x) def forward(self, x): """順伝播""" x = self.encode(x) x = self.decoder(x) return x def evaluate(model, dataloader, device, criterion): """評価に使う関数""" model.eval() running_loss = 0.0 with torch.no_grad(): for data in dataloader: # ラベルは使用しない inputs, _ = data inputs = inputs.to(device) outputs = model( inputs, ) loss = criterion(outputs, inputs) running_loss += loss.item() average_loss = running_loss / len(dataloader) return average_loss def train( model, train_dataloader, valid_dataloader, device, criterion, optimizer, num_epochs, early_stopping_patience, checkpoint_path="checkpoint.pt", ): """学習に使う関数""" print(f"Device: {device}") # Early Stopping に使うカウンタ early_stopping_patience_counter = 0 # Early Stopping に使う検証データに対する損失 early_stopping_best_val_loss = float("inf") for epoch in range(1, num_epochs + 1): model.train() running_loss = 0.0 for batch_idx, data in enumerate(train_dataloader): # ラベルは使用しない inputs, _ = data inputs = inputs.to(device) optimizer.zero_grad() outputs = model( inputs, ) loss = criterion(outputs, inputs) loss.backward() optimizer.step() running_loss += loss.item() print(f"Epoch [{epoch}/{num_epochs}], Training Loss: {running_loss / len(train_dataloader):.5f}") val_loss = evaluate(model, valid_dataloader, device, criterion) print(f"Epoch [{epoch}/{num_epochs}], Validation Loss: {val_loss:.5f}") if early_stopping_patience == -1: continue if val_loss < early_stopping_best_val_loss: early_stopping_best_val_loss = val_loss early_stopping_patience_counter = 0 # ベストなモデルとして Checkpoint を更新する checkpoint_params = { "epoch": epoch, "model_state_dict": model.state_dict(), "optimizer_state_dict": optimizer.state_dict(), "loss": val_loss, } torch.save( checkpoint_params, checkpoint_path, ) else: early_stopping_patience_counter += 1 if early_stopping_patience_counter >= early_stopping_patience: print(f"Early stopping at epoch {epoch + 1}") break print("Training Finished") def main(): # 事前にシード値を固定する set_random_seed(42) # MNIST データセットを読み込む transform = transforms.Compose( [ # PyTorch Tensor への変換と Min-Max Normalization transforms.ToTensor(), # (28, 28) -> (784,) transforms.Lambda(lambda x: torch.flatten(x)), ] ) mnist_train_dataset = datasets.MNIST( root="dataset", train=True, download=True, transform=transform, ) mnist_test_dataset = datasets.MNIST( root="dataset", train=False, download=True, transform=transform, ) # 学習用のデータセットを学習用と検証用に分割する dataset_size = len(mnist_train_dataset) val_size = int(dataset_size * 0.2) train_size = dataset_size - val_size train_dataset, valid_dataset = random_split( mnist_train_dataset, (train_size, val_size) ) # データローダを設定する batch_size = 64 train_dataloader = DataLoader( mnist_train_dataset, batch_size=batch_size, shuffle=True, ) valid_dataloader = DataLoader( valid_dataset, batch_size=batch_size, shuffle=False, ) test_dataloader = DataLoader( mnist_test_dataset, batch_size=batch_size, shuffle=False, ) # 最大エポック数 num_epochs = 1_000 # 改善が見られなかった場合に停止する Early Stopping のエポック数 early_stopping_patience = 5 # 学習に使うデバイス device = computing_device() # モデル model = AutoEncoder() model = model.to(device) # 損失関数 criterion = nn.MSELoss() # オプティマイザ optimizer = optim.Adam(model.parameters()) # 途中結果を記録するパス checkpoint_path = "MNIST-AE.pt" # 学習する train( model, train_dataloader, valid_dataloader, device, criterion, optimizer, num_epochs, early_stopping_patience, checkpoint_path, ) # ベストなモデルをロードする checkpoint = torch.load(checkpoint_path) model.load_state_dict(checkpoint["model_state_dict"]) best_epoch = checkpoint["epoch"] best_val_loss = checkpoint["loss"] # テストデータを評価する test_loss = evaluate( model, test_dataloader, device, criterion, ) print(f"Epoch: {best_epoch}, Validation Loss: {best_val_loss:.5f}") print(f"Test Set Evaluation - Loss: {test_loss:.5f}") # テストデータに対する結果を可視化する model.eval() # 最初のミニバッチを取り出す mini_batch = next(iter(test_dataloader)) # ミニバッチのデータをモデルに通す inputs, labels = mini_batch inputs = inputs.to(device) with torch.no_grad(): outputs = model( inputs, ).to("cpu") encoded = model.encode( inputs, ).to("cpu") # ランダムに 10 点をサンプリングして可視化する sample_indices = random.sample(range(mini_batch[0].shape[0]), 10) fig, axes = plt.subplots(3, 10) for i, idx in enumerate(sample_indices): # 元の画像 (28 x 28) orig_img = mini_batch[0][idx].reshape(28, 28) axes[0][i].imshow(orig_img, cmap="gray") axes[0][i].axis("off") axes[0][i].set_title(labels[idx].numpy(), color="red") # ボトルネック部分での表現 (8 x 4) enc_img = encoded[idx].reshape(8, 4) axes[1][i].imshow(enc_img, cmap="gray") axes[1][i].axis("off") # 復元した画像 (28 x 28) pred_img = outputs[idx].reshape(28, 28) axes[2][i].imshow(pred_img, cmap="gray") axes[2][i].axis("off") plt.savefig("mnistae.png") plt.show() if __name__ == "__main__": main()
上記を実行する。 エポックを重ねる毎に少しずつ損失が減っていく。
$ python mnistae.py Device: mps Epoch [1/1000], Training Loss: 0.04848 Epoch [1/1000], Validation Loss: 0.02846 Epoch [2/1000], Training Loss: 0.02480 Epoch [2/1000], Validation Loss: 0.02163 Epoch [3/1000], Training Loss: 0.01990 Epoch [3/1000], Validation Loss: 0.01821 ... Epoch [78/1000], Training Loss: 0.00544 Epoch [78/1000], Validation Loss: 0.00538 Epoch [79/1000], Training Loss: 0.00542 Epoch [79/1000], Validation Loss: 0.00542 Epoch [80/1000], Training Loss: 0.00541 Epoch [80/1000], Validation Loss: 0.00536 Early stopping at epoch 81 Training Finished Epoch: 75, Validation Loss: 0.00532 Test Set Evaluation - Loss: 0.00542
実行が完了すると次のような可視化が得られる。
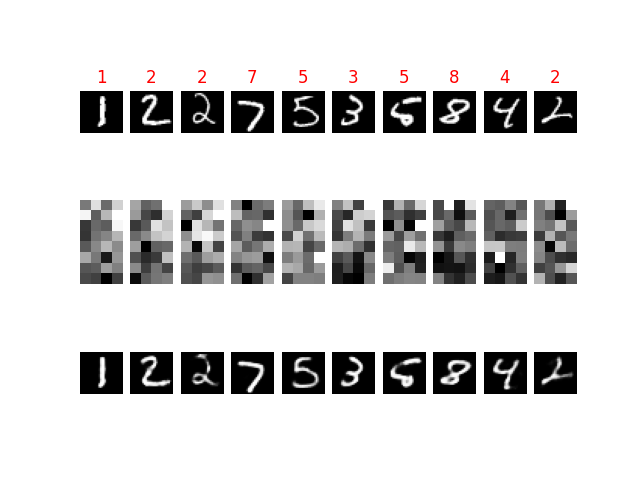
それぞれ、以下のような意味がある。
- 上段はモデルの入力となった画像を表している
- 中段はモデルのボトルネック部分において圧縮された表現を可視化したもの
- 下段はモデルが出力した画像を表している