CUBE SUGAR CONTAINER

技術系のこと書きます。

Python: PyTorch で Adam を実装してみる

PyTorch Python NeuralNetwork 機械学習

今回は、以下の記事の続きとして PyTorch で Adam を実装してみる。

blog.amedama.jp

Adam は、その収束の早さなどから利用されることの多い代表的なオプティマイザのひとつになっている。

使った環境は次のとおり。

$ sw_vers
ProductName:        macOS
ProductVersion:     15.2
BuildVersion:       24C101
$ python -V          
Python 3.12.7
$ pip list | egrep -i "(torch|matplotlib)"
matplotlib        3.9.2
torch             2.5.1

もくじ

下準備

あらかじめ PyTorch と Matplotlib をインストールしておく。

$ pip install torch matplotlib

PyTorch 組み込みの Adam を試す

まずは PyTorch に組み込みで用意されている Adam の振る舞いを確認する。

以下にサンプルコードを示す。 扱う問題は先に示した記事と同じもの。 問題設定や初期値などは「ゼロから作るDeep Learning1」に記載されている内容と揃えている。 サンプルコードでは、関数の出力をゼロに近づけるようにパラメータを更新していく。

import torch
from matplotlib import pyplot as plt
from torch import nn
from torch import optim


class ExampleFunction(nn.Module):

    def __init__(self, a, x, b, y):
        super(ExampleFunction, self).__init__()
        self.a = a
        self.x = nn.Parameter(torch.tensor([x]))
        self.b = b
        self.y = nn.Parameter(torch.tensor([y]))

    def forward(self):
        return self.a * self.x**2 + self.b * self.y**2


def main():
    model = ExampleFunction(a=1 / 20, x=-7.0, b=1.0, y=2.0)

    optimizer = optim.Adam(model.parameters(), lr=0.3)

    trajectory_x = [model.x.detach().numpy()[0]]
    trajectory_y = [model.y.detach().numpy()[0]]

    num_epochs = 30
    for epoch in range(1, num_epochs + 1):
        optimizer.zero_grad()

        outputs = model()

        outputs.backward()

        optimizer.step()

        x = model.x.detach().numpy()[0]
        trajectory_x.append(x)
        y = model.y.detach().numpy()[0]
        trajectory_y.append(y)

    fig, ax = plt.subplots(1, 1, figsize=(8, 8))
    ax.plot(trajectory_x, trajectory_y, marker="o", markersize=5, label="Trajectory")
    ax.legend()
    ax.grid(True)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    plt.show()


if __name__ == "__main__":
    main()

上記に適当な名前をつけて保存した上で実行する。

$ python torchadam.py

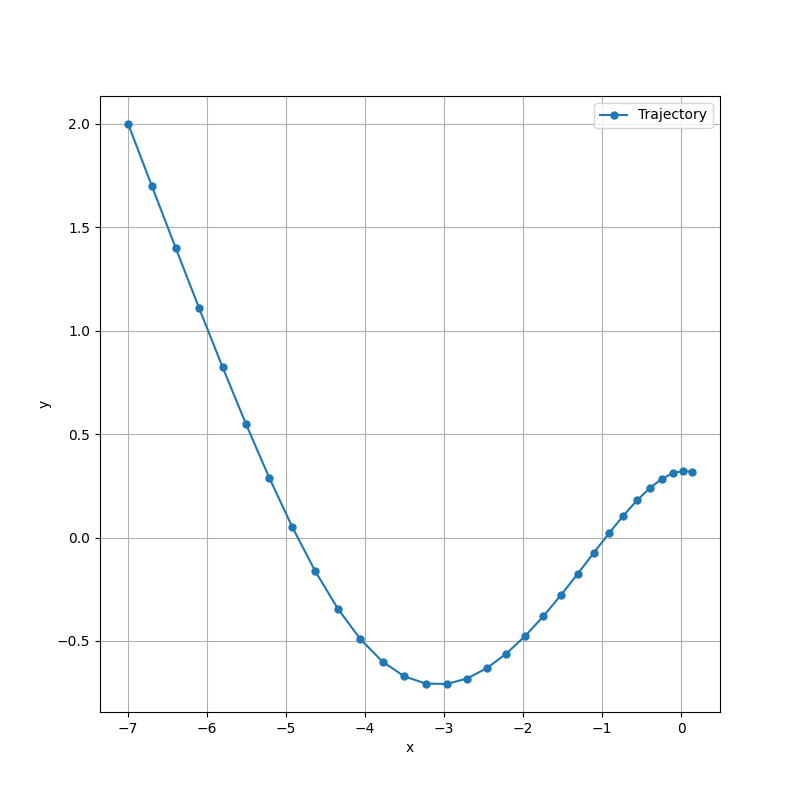
すると、以下のようなグラフが得られる。 これは、パラメータが更新されてゼロに近づいていく過程を表している。 このパラメータが更新される振る舞いがオプティマイザのアルゴリズムによって異なっている。

PyTorch 組み込みの Adam で最適化したパラメータの軌跡

Adam のオプティマイザを自作する

続いては Adam のオプティマイザを自作してみる。 サンプルコードを以下に示す。 サンプルコードでは CustomAdam という名前でオプティマイザを実装している。

from collections.abc import Iterable
from typing import Any

import torch
from matplotlib import pyplot as plt
from torch import nn
from torch.optim import Optimizer


class ExampleFunction(nn.Module):

    def __init__(self, a, x, b, y):
        super(ExampleFunction, self).__init__()
        self.a = a
        self.x = nn.Parameter(torch.tensor([x]))
        self.b = b
        self.y = nn.Parameter(torch.tensor([y]))

    def forward(self):
        return self.a * self.x**2 + self.b * self.y**2


class CustomAdam(Optimizer):
    """自作した Adam のオプティマイザ"""

    def __init__(
        self,
        params: Iterable,
        lr: float = 1e-3,
        beta1: float = 0.9,
        beta2: float = 0.999,
        eps: float = 1e-8,
    ):
        defaults: dict[str, Any] = dict(
            lr=lr,
            beta1=beta1,
            beta2=beta2,
            eps=eps,
        )
        super(CustomAdam, self).__init__(params, defaults)

    def step(self, closure=None):
        for group in self.param_groups:
            beta1 = group["beta1"]
            beta2 = group["beta2"]
            eps = group["eps"]

            # beta_1 をイテレーション数だけ乗算する変数
            if "beta1_t" not in self.state:
                self.state["beta1_t"] = torch.tensor(1.)
            self.state["beta1_t"] *= beta1

            # beta_2 をイテレーション数だけ乗算する変数
            if "beta2_t" not in self.state:
                self.state["beta2_t"] = torch.tensor(1.)
            self.state["beta2_t"] *= beta2

            for param in group["params"]:
                if param.grad is None:
                    continue
                """
                (更新式)
                m_0 = 0
                v_0 = 0
                g_{t+1} = grad(L(theta_t))
                m_{t+1} = beta1 * m_t + (1 - beta1) * g_{t+1}
                v_{t+1} = beta2 * v_t + (1 - beta2) * g_{t+1}^2
                hat{m_{t+1}} = m_{t+1} / (1 - beta1^t)
                hat{v_{t+1}} = v_{t+1} / (1 - beta2^t)
                theta_{t+1} = theta_t - alpha * (hat{m_{t+1}} / (sqrt{hat{v_{t+1}}} + eps))

                theta: パラメータ (重み)
                alpha: 学習率
                grad(L(theta)): 損失関数の勾配
                m: 指数移動平均で求めた勾配の 1 次モーメント
                v: 指数移動平均で求めた勾配の 2 次モーメント
                beta1: 指数移動平均で勾配の 1 次モーメントを求める際の係数
                beta2: 指数移動平均で勾配の 2 次モーメントを求める際の係数
                eps: ゼロ除算を防ぐ小さな値
                """
                # m_0 = 0 に対応する
                if "m" not in self.state[param]:
                    self.state[param]["m"] = torch.zeros_like(param.data)
                # v_0 = 0 に対応する
                if "v" not in self.state[param]:
                    self.state[param]["v"] = torch.zeros_like(param.data)

                # m_{t+1} = beta1 * m_t + (1 - beta1) * g_{t+1} に対応する
                self.state[param]["m"] = beta1 * self.state[param]["m"] + (1 - beta1) * param.grad
                # v_{t+1} = beta2 * v_t + (1 - beta2) * g_{t+1}^2 に対応する
                self.state[param]["v"] = beta2 * self.state[param]["v"] + (1 - beta2) * param.grad ** 2

                # hat{m_{t+1}} = m_{t+1} / (1 - beta1^t) に対応する
                # beta1^t は self.state["beta1_t"] で計算している
                m_hat = self.state[param]["m"] / (1 - self.state["beta1_t"])
                # hat{v_{t+1}} = v_{t+1} / (1 - beta2^t) に対応する
                # beta2^t は self.state["beta2_t"] で計算している
                v_hat = self.state[param]["v"] / (1 - self.state["beta2_t"])

                # theta_{t+1} = theta_t - alpha * (hat{m_{t+1}} / (sqrt{hat{v_{t+1}}} + eps)) に対応する
                param.data -= group["lr"] * (m_hat / (torch.sqrt(v_hat) + eps))


def main():
    model = ExampleFunction(a=1 / 20, x=-7.0, b=1.0, y=2.0)

    optimizer = CustomAdam(model.parameters(), lr=0.3)

    trajectory_x = [model.x.detach().numpy()[0]]
    trajectory_y = [model.y.detach().numpy()[0]]

    num_epochs = 30
    for epoch in range(1, num_epochs + 1):
        optimizer.zero_grad()

        outputs = model()

        outputs.backward()

        optimizer.step()

        x = model.x.detach().numpy()[0]
        trajectory_x.append(x)
        y = model.y.detach().numpy()[0]
        trajectory_y.append(y)

    fig, ax = plt.subplots(1, 1, figsize=(8, 8))
    ax.plot(trajectory_x, trajectory_y, marker="o", markersize=5, label="Trajectory")
    ax.legend()
    ax.grid(True)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    plt.show()


if __name__ == "__main__":
    main()

上記に適当な名前をつけて実行する。

$ python customadam.py

すると、次のようなグラフが得られる。

自作した Adam で最適化したパラメータの軌跡

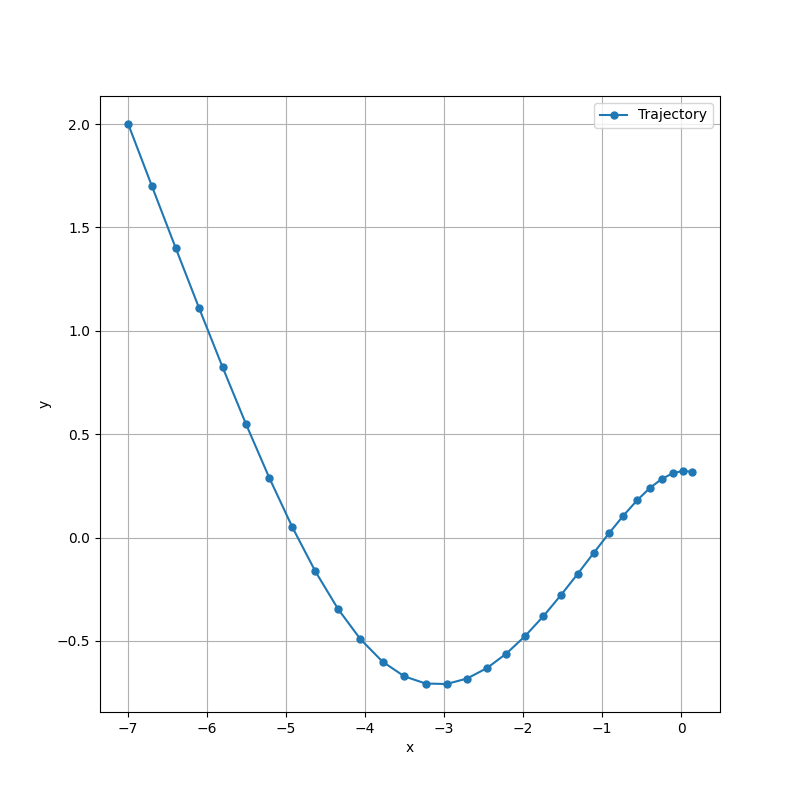
グラフから、PyTorch に組み込みで用意されている Adam と同じ軌跡を辿っていることが確認できる。

更新式とコードの対応関係について

ここからは更新式とコードについて見ていく。

Adam の更新式は以下のようになっている。

\displaystyle m_0 = 0 \\ v_0 = 0 \\ g_{t+1} = \nabla_{\theta} L(\theta_t) \\ m_{t+1} = \beta_1 m_t + (1 - \beta_1) g_{t+1} \\ v_{t+1} = \beta_2 v_t + (1 - \beta_2) g_{t+1}^2 \\ \hat{m_{t+1}} = \frac{m_{t+1}}{1 - \beta_1^{t+1}} \\ \hat{v_{t+1}} = \frac{v_{t+1}}{1 - \beta_2^{t+1}} \\ \theta_{t+1} = \theta_t - \alpha \frac{\hat{m_{t+1}}}{\sqrt{\hat{v_{t+1}}} + \epsilon}

数式と、プログラムの変数の対応関係は次のとおり。

  • \theta
    • param.data
  • \alpha
    • group["lr"]
  • \nabla_{\theta} L(\theta)
    • param.grad
  • \beta_1
    • beta1
  • \beta_2
    • beta2
  • m
    • self.state[param]["m"]
  • v
    • self.state[param]["v"]
  • \epsilon
    • group["eps"]
  • t
    • self.state["t"]

式から、 m や v が、いずれも勾配を元に指数移動平均を求める形になっていることが分かる。 m についてはそのまま、 v については二乗しているため、それぞれ 1 次モーメントと 2 次モーメントを表しているらしい。 これらの値にイテレーション回数に関するバイアス補正をかけた上で、スケール調整したものを使ってパラメータを更新する。

直感的には、過去の勾配の情報が次の更新に強く影響するように感じられる。 たとえば一度勢いがつくと、なかなかその方向への更新が止まりにくいはず。 この点は勢いよく更新した方が、大局的にはパラメータが早く収束するのかもしれない。 また、汎化性能を得やすいとされる損失関数の平坦解にも到達しやすいのだろう。

ここからはコードとの対応関係を見ていこう。 まずは以下の更新式に対応するコードから。

\displaystyle m_0 = 0 \\ v_0 = 0

ここでは m や v がまだ無い状態、つまり初期状態のときに変数をゼロで初期化している。

                # m_0 = 0 に対応する
                if "m" not in self.state[param]:
                    self.state[param]["m"] = torch.zeros_like(param.data)
                # v_0 = 0 に対応する
                if "v" not in self.state[param]:
                    self.state[param]["v"] = torch.zeros_like(param.data)

次に以下の更新式に対応するコード。

\displaystyle g_{t+1} = \nabla_{\theta} L(\theta_t) \\ m_{t+1} = \beta_1 m_t + (1 - \beta_1) g_{t+1} \\ v_{t+1} = \beta_2 v_t + (1 - \beta_2) g_{t+1}^2

ここでは指数移動平均で勾配の 1 次モーメントと 2 次モーメントを計算している。

                # m_{t+1} = beta1 * m_t + (1 - beta1) * g_{t+1} に対応する
                self.state[param]["m"] = beta1 * self.state[param]["m"] + (1 - beta1) * param.grad
                # v_{t+1} = beta2 * v_t + (1 - beta2) * g_{t+1}^2 に対応する
                self.state[param]["v"] = beta2 * self.state[param]["v"] + (1 - beta2) * param.grad ** 2

次に以下の更新式に対応するコード。

\displaystyle \hat{m_{t+1}} = \frac{m_{t+1}}{1 - \beta_1^{t+1}} \\ \hat{v_{t+1}} = \frac{v_{t+1}}{1 - \beta_2^{t+1}}

ここではバイアス補正をしている。 イテレーション数がゼロのときは各モーメントがゼロから始まるので、そのままでは更新量が少なくなってしまう。 そこでイテレーション回数が少ないうちは更新量を多く、回数が多くなるほど更新量を抑えるように調整している。

                # hat{m_{t+1}} = m_{t+1} / (1 - beta1^t) に対応する
                # beta1 ** t は self.state["beta1_t"] で計算している
                m_hat = self.state[param]["m"] / (1 - self.state["beta1_t"])
                # hat{v_{t+1}} = v_{t+1} / (1 - beta2^t) に対応する
                # beta2 ** t は self.state["beta2_t"] で計算している
                v_hat = self.state[param]["v"] / (1 - self.state["beta2_t"])

なお、 \beta_1^{t+1} や \beta_2^{t+1} の部分は以下のように求めている。 これは、イテレーション毎に改めて計算していると無駄な計算が生じるため。

            # beta_1 をイテレーション数だけ乗算する変数
            if "beta1_t" not in self.state:
                self.state["beta1_t"] = torch.tensor(1.)
            self.state["beta1_t"] *= beta1

            # beta_2 をイテレーション数だけ乗算する変数
            if "beta2_t" not in self.state:
                self.state["beta2_t"] = torch.tensor(1.)
            self.state["beta2_t"] *= beta2

そして、最後に以下の更新式に対応するコード。

\displaystyle \theta_{t+1} = \theta_t - \alpha \frac{\hat{m_{t+1}}}{\sqrt{\hat{v_{t+1}}} + \epsilon}

ここでは 1 次モーメントを 2 次モーメントの平方根でスケール調整した値でパラメータを更新している。

                # theta_{t+1} = theta_t - alpha * (hat{m_{t+1}} / (sqrt{hat{v_{t+1}}} + eps)) に対応する
                param.data -= group["lr"] * (m_hat / (torch.sqrt(v_hat) + eps))

いじょう。

参考

arxiv.org

arxiv.org

Linuxで動かしながら学ぶTCP/IPネットワーク入門

Linuxで動かしながら学ぶTCP/IPネットワーク入門

Amazon

  1. https://www.oreilly.co.jp/books/9784873117584/↩