今回は、以下の記事の続きとして PyTorch で Adagrad を実装したオプティマイザを自作してみる。 以下の記事では単純な SGD と Momentum を導入した SGD を実装した。
今回扱う Adagrad のアルゴリズムではパラメータごとに学習率を自動で調整する。 これによって値の収束が早まったり、あるいは過剰に値が更新されることを防ぐことができる。 ただし、学習率の調整に過去の勾配の平方和だけを使っていることから、徐々に学習が進みにくくなってしまう問題がある。 この問題を解決するために RMSProp が提案された。
使った環境は次のとおり。
$ sw_vers ProductName: macOS ProductVersion: 14.6.1 BuildVersion: 23G93 $ python -V Python 3.11.9 $ pip list | egrep -i "(torch|matplotlib)" matplotlib 3.9.2 torch 2.4.1
もくじ
下準備
下準備として PyTorch と Matplotlib をインストールしておく。
$ pip install torch matplotlib
PyTorch 組み込みの Adagrad を試す
まずは PyTorch 組み込みの Adagrad の動作を確認する。 扱う問題は先に示した記事と同じもの。 この問題設定や初期値などは「ゼロから作るDeep Learning 1」に記載されている内容と同一にしている。
import torch from matplotlib import pyplot as plt from torch import nn from torch import optim class ExampleFunction(nn.Module): """最適化したい関数: f(x, y) = ax^2 + by^2""" def __init__(self, a, x, b, y): super(ExampleFunction, self).__init__() self.a = a self.x = nn.Parameter(torch.tensor([x])) self.b = b self.y = nn.Parameter(torch.tensor([y])) def forward(self): # f(x, y) = ax^2 + by^2 return self.a * self.x**2 + self.b * self.y**2 def main(): # 初期値を指定して最適化したいモデルをインスタンス化する model = ExampleFunction(a=1 / 20, x=-7.0, b=1.0, y=2.0) # Adagrad で最適化する optimizer = optim.Adagrad(model.parameters(), lr=1.5) # パラメータの軌跡を残す trajectory_x = [model.x.detach().numpy()[0]] trajectory_y = [model.y.detach().numpy()[0]] # 最適化のループを 30 回にわたって回す num_epochs = 30 for epoch in range(1, num_epochs + 1): # 勾配を初期化する optimizer.zero_grad() # モデルの出力を得る outputs = model() # 誤差逆伝播 # 本来は損失関数を元に勾配を求める # 今回はパラメータがゼロへ近づくように最適化する outputs.backward() # パラメータを更新する optimizer.step() # 更新されたパラメータを記録する x = model.x.detach().numpy()[0] trajectory_x.append(x) y = model.y.detach().numpy()[0] trajectory_y.append(y) # パラメータのたどった軌跡を可視化する fig, ax = plt.subplots(1, 1, figsize=(8, 6)) ax.plot(trajectory_x, trajectory_y, marker="o", markersize=5, label="Trajectory") ax.legend() ax.grid(True) ax.set_xlabel("x") ax.set_ylabel("y") plt.show() if __name__ == "__main__": main()
上記に適当な名前をつけて実行する。
$ python adagrad.py
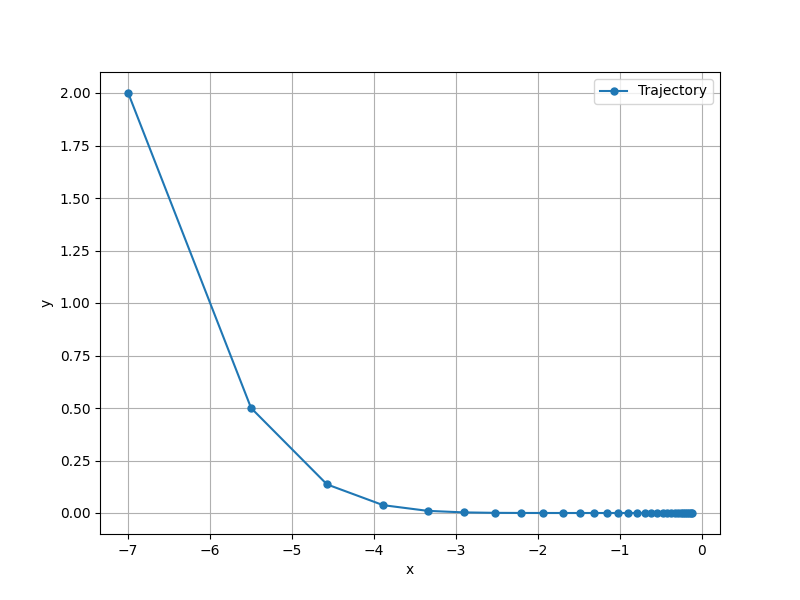
すると、次のようなグラフが得られる。 これは、パラメータが更新されていく様子を表している。
Adagrad のアルゴリズムを実装する
続いては Adagrad のオプティマイザを自作してみよう。
早速だけどサンプルコードを以下に示す。
サンプルコードでは CustomAdagrad という名前でオプティマイザを実装している。
オプティマイザを実装する際の流儀や API については先に示した記事を参照してもらいたい。
from collections.abc import Iterable from typing import Any import torch from matplotlib import pyplot as plt from torch import nn from torch.optim import Optimizer class ExampleFunction(nn.Module): def __init__(self, a, x, b, y): super(ExampleFunction, self).__init__() self.a = a self.x = nn.Parameter(torch.tensor([x])) self.b = b self.y = nn.Parameter(torch.tensor([y])) def forward(self): return self.a * self.x**2 + self.b * self.y**2 class CustomAdagrad(Optimizer): """自作した Adagrad のオプティマイザ""" def __init__(self, params: Iterable, lr: float = 1e-3, eps=1e-10): defaults: dict[str, Any] = dict( lr=lr, eps=eps, ) super(CustomAdagrad, self).__init__(params, defaults) def step(self, closure=None): """Adagrad の更新式を実装した step() メソッド (更新式) v_0 = 0 v_{t+1} = v_t + grad(L(theta_t))^2 theta_{t+1} = theta_t - eta / (sqrt(v_{t+1}) + eps) * grad(L(theta_t)) theta: パラメータ (重み) eta: 学習率 grad(L(theta)): 損失関数の勾配 v: 過去の勾配の平方和 eps: ゼロ除算を防ぐための小さな値 """ for group in self.param_groups: for param in group["params"]: if param.grad is None: continue # v_0 = 0 に対応する if "v" not in self.state[param]: self.state[param]["v"] = torch.zeros_like(param.data) # v_{t+1} = v_t + grad(L(theta_t))^2 に対応する self.state[param]["v"] += param.grad * param.grad # theta_{t+1} = theta_t - eta / (sqrt(v_{t+1}) + eps) * grad(L(theta_t)) に対応する param.data -= group["lr"] / (torch.sqrt(self.state[param]["v"]) + group["eps"]) * param.grad def main(): model = ExampleFunction(a=1 / 20, x=-7.0, b=1.0, y=2.0) # 自作したオプティマイザを使う optimizer = CustomAdagrad(model.parameters(), lr=1.5) trajectory_x = [model.x.detach().numpy()[0]] trajectory_y = [model.y.detach().numpy()[0]] num_epochs = 30 for epoch in range(1, num_epochs + 1): optimizer.zero_grad() outputs = model() outputs.backward() optimizer.step() x = model.x.detach().numpy()[0] trajectory_x.append(x) y = model.y.detach().numpy()[0] trajectory_y.append(y) fig, ax = plt.subplots(1, 1, figsize=(8, 6)) ax.plot(trajectory_x, trajectory_y, marker="o", markersize=5, label="Trajectory") ax.legend() ax.grid(True) ax.set_xlabel("x") ax.set_ylabel("y") plt.show() if __name__ == "__main__": main()
上記に適当な名前をつけて実行してみよう。
$ python customadagrad.py
すると、以下のグラフが得られる。
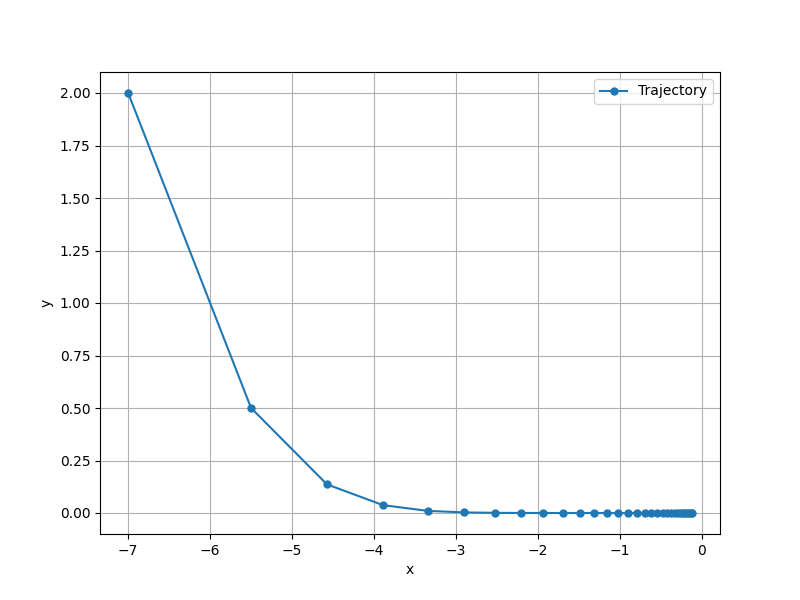
上記から PyTorch 組み込みの実装と振る舞いが一致していることが確認できる。
更新式とコードの対応関係
ここからは更新式とコードについて見ていく。 まず、Adagrad の更新式は以下のようになっている。
数式と、プログラムの変数の対応関係は次のとおり。
param.data
group["lr"]
param.grad
self.state[param]["v"]
group["eps"]
式から、 には勾配の平方和が蓄積されていくことが分かる。
そして、学習率と勾配から更新量を求める部分に
として挟まっていることが分かる。
これによって、過去の勾配を元にパラメータの更新される大きさが決まるようになっている。
逆数なので、分母が大きくなるほど更新される量は減っていく。
そして、
は単純に増加していくので、イテレーションが進むごとに更新される量が減ることが分かる。
はパラメータごとにあるので、過去に大きな勾配が求められた (= すでに大きく更新された) ものはなるべく更新されないように振る舞う。
コードとの対応関係を見ていこう。 まずは、以下の更新式に対応するコードから。
ここでは がまだない状態、つまり初期状態のとき変数をゼロで初期化している。
# v_0 = 0 に対応する if "v" not in self.state[param]: self.state[param]["v"] = torch.zeros_like(param.data)
続いては以下の更新式に対応するコード。
ここでは求められたパラメータの勾配の二乗を、先ほど初期化した変数に足している。
# v_{t+1} = v_t + grad(L(theta_t))^2 に対応する self.state[param]["v"] += param.grad * param.grad
最後に、以下の更新式に対応するコード。
ここでは先ほど求めた を使ってパラメータを更新している。
# theta_{t+1} = theta_t - eta / (sqrt(v_{t+1}) + eps) * grad(L(theta_t)) に対応する param.data -= group["lr"] / (torch.sqrt(self.state[param]["v"]) + group["eps"]) * param.grad
いじょう。
