Python: k-NN Feature Extraction について

k-NN Feature Extraction (k-近傍法を用いた特徴量抽出) という手法があるらしい。 これは、文字通り k-NN (k-Nearest Neighbor algorithm: k-近傍法) を特徴量の抽出に応用したもの。 興味深かったので、今回は自分でも Python を使って実装してみた。 手法について知ったのは、以下のブログを目にしたのがきっかけ。

upura.hatenablog.com

また、上記は以下のブログに記載のある R の実装を参考にしているとのことだった。

Feature Extraction with KNN • fastknn

ただ、先ほどの Python API では、特徴量を付与する対象のデータをパラメータとして指定できない点が気になった。 具体的には、以下のような交差検証を使った性能の計測が難しいのではと感じた。

• データセットを学習用と検証用に分割する
• 学習用データに対して k-NN Feature Extraction で特徴量を付与する
  • 付与するデータと付与に使うデータに分けながら順番に付与していく
• 特徴量が付与された学習用データを使ってモデルを学習させる
• 学習用データを使って検証用データに k-NN Feature Extraction で特徴量を付与する
• 特徴量が付与された検証用データを使ってモデルの性能を計測する

R の実装では、特徴量を付与するデータと付与に使うデータを別々に指定できる。 そこで、今回書いてみたものは R の実装にならって別々に指定できるようにしてみた。

使った環境は次の通り。

$ sw_vers 
ProductName:    Mac OS X
ProductVersion: 10.13.6
BuildVersion:   17G3025
$ python -V
Python 3.7.1

k-NN Feature Extraction について

ここからは k-NN Feature Extraction の具体的な手法について解説していく。 まず、k-NN Feature Extraction では、名前の通り k-NN (k-近傍法) を特徴量の抽出に応用している。 元々の k-NN は分類問題を解くためのアルゴリズムだった。

最初に k-NN では、分類したい対象のデータから最も近い k 点の学習データを探し出す。 k 点の k には 1 や 3 など、任意の数を用いる。 最も近い k 点の学習データが見つかったら、その学習データについているクラスを使って対象のデータを分類する。 k が 1 より大きいときは、多数決などを使って分類先のクラスを決める。

k-NN Feature Extraction では、上記のアルゴリズムのうち前半部分だけを利用する。 具体的には、最も近い k 点の学習データを探し出す部分。 このとき、最も近い k 点の学習データを探すために、データ間の距離を計算することになる。 k-NN Feature Extraction では、このデータ間の距離を特徴量として用いる。

少し k-NN と異なるのは、k 点の近傍データを探すのがクラスごとという点。 つまり、二値分類問題であれば、学習データの中のクラス 0 とクラス 1 ごとに近傍データをそれぞれ探す。 もちろん多値分類問題であれば、クラス数 c の数だけ近傍データを探すことになる。 さらに、k が 1 を越える場合には、1 ~ k までの全ての数で近傍データを探すようだ。 これによって k * c 個の特徴量が新たに生成されることになる。

文章だけだとなかなか分かりにくいと思うので図示してみる。 まず、以下のような感じで特徴量を付与したいデータとクラスが三つに分かれた学習データがあるとする。

特徴量を付与したいデータから、それぞれのクラスの近傍データまでの距離を計算して特徴量にする。

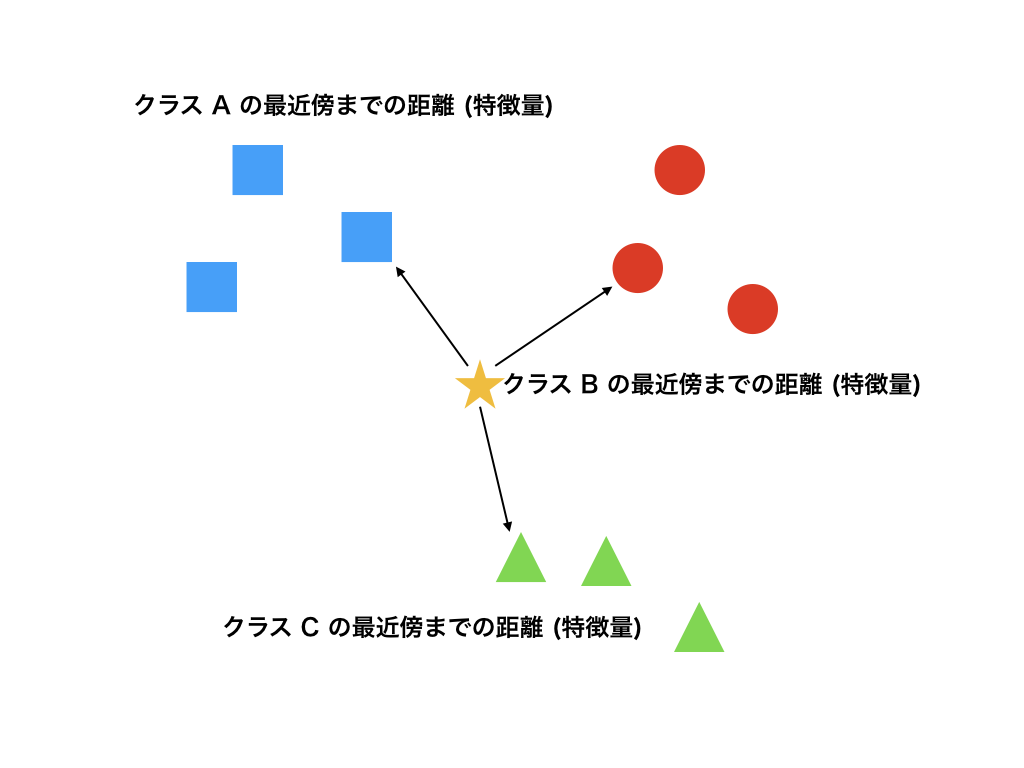
もし k > 1 であれば、複数の近傍点までの距離を足し合わせたものを特徴量にする。

いじょう。

下準備

実際に実装してみる前に、必要なパッケージを環境にインストールしておく。

$ pip install scikit-learn matplotlib

サンプルデータについて

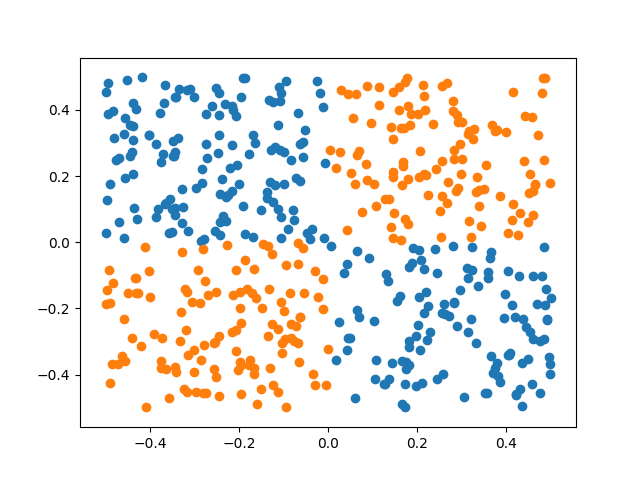
特徴量の付与に使うサンプルデータについては、以下のような線形分離できないものを用いた。

上記を生成したのは次のようなサンプルコードになる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
from matplotlib import pyplot as plt


def main():
    # サンプルデータを生成する
    x0 = np.random.rand(500) - 0.5
    x1 = np.random.rand(500) - 0.5
    X = np.array(list(zip(x0, x1)))
    y = np.array([1 if i0 * i1 > 0 else 0 for i0, i1 in X])

    # データを可視化する
    plt.scatter(X[y == 0, 0], X[y == 0, 1])
    plt.scatter(X[y == 1, 0], X[y == 1, 1])
    plt.show()


if __name__ == '__main__':
    main()

適当な名前をつけて実行すると、先ほどのグラフが出力される。

$ python visualize.py

k-NN Feature Extraction で特徴量を抽出してみる

それでは、実際に k-NN Feature Extraction を試してみよう。 以下のサンプルコードの knn_extract() 関数が特徴量を生成する関数になる。 基本的な使い方としては、学習データとしてxtr と、そのクラスデータとして ytr を渡す。 そして、特徴量を生成する対象のデータとして xte を渡す。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import functools
from concurrent.futures import ProcessPoolExecutor
import multiprocessing

import numpy as np
from sklearn.model_selection import KFold
from matplotlib import pyplot as plt


def _distance(a, b):
    """2 点間の距離を計算する"""
    distance = np.linalg.norm(a - b)
    return distance


def _knn_distance(xtr_c, target, k):
    """特定クラスの最近傍な教師データへの距離を計算する"""
    # 各要素への距離を計算する
    distances = np.array([_distance(target, x) for x in xtr_c])
    # 距離で昇順ソートする
    sorted_distances = np.sort(distances)
    # 先頭 k 件を取り出す (最近傍への距離 k 点)
    nearest_distances = sorted_distances[:k]
    # 距離を足し算して返す
    sum_distances = np.sum(nearest_distances)
    return sum_distances


def _knn_distance_fold(xtr_c, k, folds, target):
    """過学習を防ぐためにサンプリングしながら最近傍への距離の平均を計算する"""
    # 途中までの計算結果を代入するための入れ物
    distances = np.empty([folds])

    # K-分割することでサンプリングする
    kf = KFold(shuffle=True, n_splits=folds)
    for i, (train_index, _) in enumerate(kf.split(xtr_c)):
        # サンプリングした教師信号
        xtr_c_sampled = xtr_c[train_index]
        # ターゲットと教師信号との距離を計算する
        distance = _knn_distance(xtr_c_sampled, target, k)
        distances[i] = distance

    # 各サンプルでの距離の平均を返す
    average_distance = distances.mean()
    return average_distance


def knn_extract(xtr, ytr, xte, k=1, folds=5, nprocesses=-1):
    if nprocesses == -1:
        # デフォルトでは CPU のコア数で並列計算する
        nprocesses = multiprocessing.cpu_count()

    # 教師データに含まれているクラス (ラベル) の種類
    # NOTE: CV するときは含まれるクラスが偏らないようにすること
    classes = np.unique(ytr)

    # 生成する特徴量の入れ物を用意する
    features = np.zeros([len(xte), len(classes) * k])

    for i, class_ in enumerate(classes):
        # 処理対象のクラス
        xtr_c = xtr[ytr == class_]

        for j, k_n in enumerate(range(1, k + 1), 1):
            # クラス class_ で近傍数 k の距離を計算する関数に実引数を部分適用する
            f = functools.partial(_knn_distance_fold, xtr_c, k_n, folds)

            # クラス class_ で近傍数 k で計算した特徴ベクトル
            with ProcessPoolExecutor(max_workers=nprocesses) as executor:
                feature = executor.map(f, xte)
                features[:, i * j] = list(feature)

    return features


def main():
    # サンプルデータを生成する
    x0 = np.random.rand(500) - 0.5
    x1 = np.random.rand(500) - 0.5
    X = np.array(list(zip(x0, x1)))
    y = np.array([1 if i0 * i1 > 0 else 0 for i0, i1 in X])

    classes = np.unique(y)
    k = 1
    extracted_features = np.empty([0, len(classes) * k])

    # データを 5 分割して、それぞれで特徴量を作っていく
    skf = KFold(n_splits=5)
    for train_index, test_index in skf.split(X):
        # 学習用データと検証用データに分ける
        X_train, X_test = X[train_index], X[test_index]
        y_train, y_test = y[train_index], y[test_index]

        # 検証用データに対して、学習用データを使って特徴量を抽出する
        extracted_feature = knn_extract(X_train, y_train, X_test, k)
        extracted_features = np.append(extracted_features, extracted_feature, axis=0)

    # k-NN Feature Extraction の結果を可視化する
    plt.scatter(extracted_features[:, 0], extracted_features[:, 1], c=y)
    plt.show()


if __name__ == '__main__':
    main()

上記に適当な名前をつけて実行しよう。

$ python knnfe.py

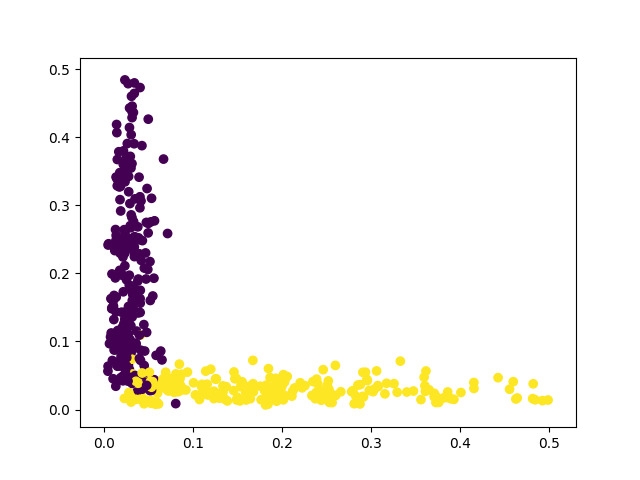
実行結果として得られるグラフは次の通り。 今回の問題は k = 1, c = 2 なので二次元の特徴量が新たに得られる。 それらを散布図にしてみると、ちゃんと線形分離できそうな形で特徴量が生成されている。

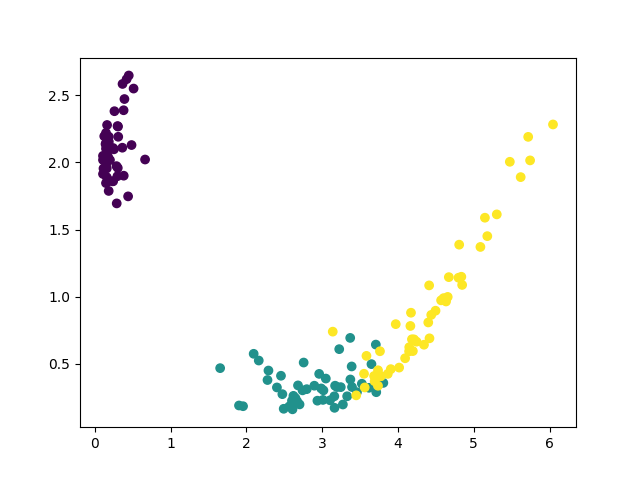
続いて Iris データセットに使ってみた場合についても紹介する。 まず、データセットの読み込み部分を以下のように変更する。

# Iris データセットを読み込む
from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data, iris.target

こちらも、四次元の特徴量から以下のような二次元の特徴量が得られる。 それなりに上手く分離できそうな雰囲気がある。

課題について

実際に試した上で気になった点としては、やはり計算量があげられる。 今回使ったようなサイズの小さいデータセットでも、実行してみると結構な時間がかかる。 これは最近傍の探索が素朴な実装になっているから。 そのため、実用上は ANN (Approximate Nearest Neighbor: 近似最近傍) を使う必要があると考えられる。

いじょう。

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ