Python: 多様体学習 (Manifold Learning) を用いた次元縮約

今回は多様体学習を使ってデータの次元を縮約する方法について。これはデータの前処理として、主に二つの目的で使われる。一つ目は、次元を縮約することで二次元や三次元の形でデータを可視化できるようにするため。もう一つは、次元を縮約した結果を教師データとして用いることでモデルの認識精度を上げられる場合があるため。

データの次元を縮約する手法としては主成分分析 (PCA) が有名だけど、これは線形な変換になっている。ただ、実際に取り扱うデータは必ずしもそれぞれの次元が線形な関係になっているとは限らない。そこで、非線形な変換をするのが多様体学習ということらしい。

今回使った環境は次の通り。

$ sw_vers      
ProductName:    Mac OS X
ProductVersion: 10.12.6
BuildVersion:   16G1114
$ python --version
Python 3.6.3

下準備

まずは、今回使う Python のライブラリをインストールしておく。

$ pip install numpy scipy scikit-learn matplotlib

扱うデータセットとしては scikit-learn の digits データセットにした。これは 8 x 8 のピクセルで表現された手書きの数値データになっている。 8 x 8 ピクセルを扱うので 64 次元になっていて、それが 1797 点ある。

>>> from sklearn import datasets
>>> dataset = datasets.load_digits()
>>> dataset.data.shape
(1797, 64)

上記のデータセットが具体的にどういったものなのかを可視化しておく。データセットからランダムに 25 点を取り出して画像として表示してみよう。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt
from matplotlib import cm
import numpy as np
from numpy import random
from sklearn import datasets


def main():
    dataset = datasets.load_digits()
    X = dataset.data
    y = dataset.target

    # データの中から 25 点を無作為に選び出す
    sample_indexes = random.choice(np.arange(len(X)), 25, replace=False)

    # 選んだデータとラベルを matplotlib で表示する
    samples = np.array(list(zip(X, y)))[sample_indexes]
    for index, (data, label) in enumerate(samples):
        # 画像データを 5x5 の格子状に配置する
        plt.subplot(5, 5, index + 1)
        # 軸に関する表示はいらない
        plt.axis('off')
        # データを 8x8 のグレースケール画像として表示する
        plt.imshow(data.reshape(8, 8), cmap=cm.gray_r, interpolation='nearest')
        # 画像データのタイトルに正解ラベルを表示する
        plt.title(label, color='red')
    # グラフを表示する
    plt.show()


if __name__ == '__main__':
    main()

上記を適当な名前をつけて保存したら実行する。

$ python digits.py

すると、次のようなグラフが得られる。 MNIST (28 x 28 ピクセル) に比べると、だいぶ荒いことが分かる。

f:id:momijiame:20171209032808p:plain

とはいえデータセットのダウンロードが生じないので取り回しが良い。

多様体学習を使ってデータセットの次元を縮約する

続いては、上記で確認したデータセットを実際に多様体学習アルゴリズムを使って次元縮約してみる。元々のデータセットは 64 次元なので、個々を画像として表示はできるものの全体を散布図のように図示することはできない。そこで、多様体学習を用いて 2 次元に縮約することで散布図として図示できるようにしてしまおう、ということ。

scikit-learn に組み込まれている多様体学習アルゴリズムの一覧は次のページで確認できる。

2.2. Manifold learning — scikit-learn 0.19.1 documentation

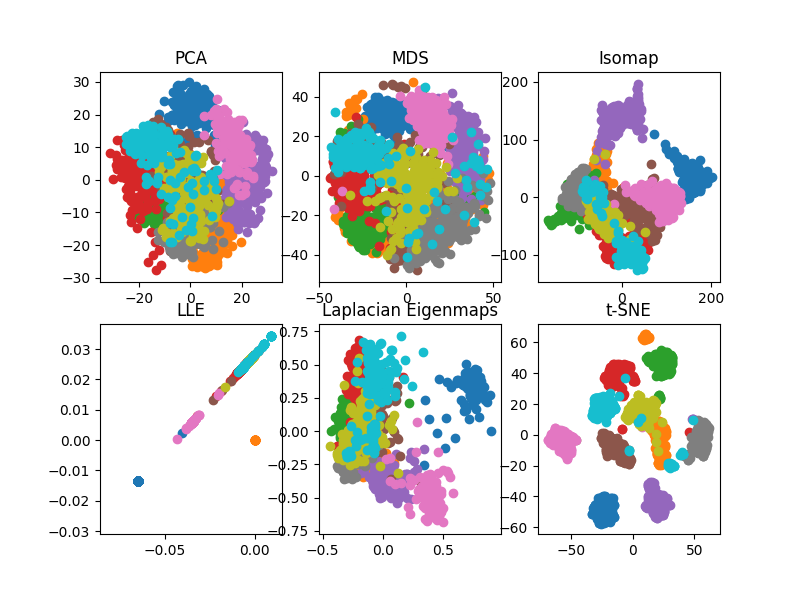
次のサンプルコードでは、上記からいくつか主要なアルゴリズムを使っている。 digits データセットの 64 次元を 2 次元に縮約した結果を散布図として図示した。一応、比較対象として主成分分析も入れている。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets

from sklearn.decomposition import PCA
from sklearn.manifold import MDS
from sklearn.manifold import LocallyLinearEmbedding
from sklearn.manifold import SpectralEmbedding
from sklearn.manifold import Isomap
from sklearn.manifold import TSNE

def main():
    dataset = datasets.load_digits()

    X = dataset.data
    y = dataset.target

    plt.figure(figsize=(12, 8))

    # 主な多様体学習アルゴリズム (と主成分分析)
    manifolders = {
        'PCA': PCA(),
        'MDS': MDS(),
        'Isomap': Isomap(),
        'LLE': LocallyLinearEmbedding(),
        'Laplacian Eigenmaps': SpectralEmbedding(),
        't-SNE': TSNE(),
    }
    for i, (name, manifolder) in enumerate(manifolders.items()):
        plt.subplot(2, 3, i + 1)

        # 多様体学習アルゴリズムを使って教師データを 2 次元に縮約する
        X_transformed = manifolder.fit_transform(X)

        # 縮約した結果を二次元の散布図にプロットする
        for label in np.unique(y):
            plt.title(name)
            plt.scatter(X_transformed[y == label, 0], X_transformed[y == label, 1])

    plt.show()

if __name__ == '__main__':
    main()

上記を適当な名前をつけて保存したら実行する。

$ python manifoldlearning.py

すると、次のようなグラフが得られる。グラフの各色は、それぞれの数字 (0 ~ 9) を表している。それぞれのクラスタがキレイにまとまった上で分かれているほど、上手く縮約できているということだと思う。この中だと t-SNE が頭一つ抜けてるなという感じ。

f:id:momijiame:20171209035139p:plain

次元を縮約した結果を教師データとして用いる

続いては多様体学習を使う目的の二つ目、認識精度の向上について見ていく。素の教師データ、主成分分析の結果、t-SNE の結果それぞれをランダムフォレストの教師データとして渡してみよう。汎化性能は、どのように変化するだろうか。

まずは素の教師データから。 digits データセットをそのままランダムフォレストに渡している。その際の精度をK-分割交差検証で確かめる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets

from sklearn.metrics import accuracy_score
from sklearn.model_selection import KFold

from sklearn.ensemble import RandomForestClassifier

def main():
    dataset = datasets.load_digits()

    X = dataset.data
    y = dataset.target

    scores = np.array([], dtype=np.bool)

    # K-分割交差検証で汎化性能を調べる (分割数は 10)
    cross_validator = KFold(n_splits=10)
    for train, test in cross_validator.split(X):
        X_train, X_test = X[train], X[test]
        y_train, y_test = y[train], y[test]

        # ランダムフォレストで素の教師データを学習する
        cls = RandomForestClassifier()
        cls.fit(X_train, y_train)

        # テストデータに対して分類する
        y_pred = cls.predict(X_test)
        scores = np.hstack((scores, y_test == y_pred))

    # テストデータに対する精度から汎化性能を求める
    accuracy_score = sum(scores) / len(scores)
    print(accuracy_score)


if __name__ == '__main__':
    main()

実行結果は次の通り。これはランダムフォレストの使う木構造の作られ方にもよるので、出力される数値は毎回微妙に異なる。今回については約 93% となった。

$ python randomforest.py 
0.929326655537

続いては主成分分析を使って次元を縮約した結果をランダムフォレストに渡すパターン。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.metrics import accuracy_score
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier


def main():
    dataset = datasets.load_digits()

    X = dataset.data
    y = dataset.target

    # 次元縮約に主成分分析を使う
    manifolder = PCA()

    scores = np.array([], dtype=np.bool)

    cross_validator = KFold(n_splits=10)
    for train, test in cross_validator.split(X):
        # 教師データを主成分分析を使って次元縮約する
        X_transformed = manifolder.fit_transform(X)

        X_train, X_test = X_transformed[train], X_transformed[test]
        y_train, y_test = y[train], y[test]

        # 縮約した教師データを学習する
        cls = RandomForestClassifier()
        cls.fit(X_train, y_train)

        y_pred = cls.predict(X_test)
        scores = np.hstack((scores, y_test == y_pred))

    accuracy_score = sum(scores) / len(scores)
    print(accuracy_score)


if __name__ == '__main__':
    main()

実行結果は次の通り。残念ながら精度は約 87% に低下してしまった。

$ python randomforestpca.py 
0.870339454647

これは、元々のデータセットの性質が非線形なため上手く主成分を取り出すことができなかったということだろう。まあ、可視化した段階でもそれぞれのクラスタがごちゃっと固まってたしね。

続いては t-SNE を使った場合。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.manifold import TSNE
from sklearn.metrics import accuracy_score
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier


def main():
    dataset = datasets.load_digits()

    X = dataset.data
    y = dataset.target

    # 次元縮約に t-SNE を使う
    manifolder = TSNE()

    scores = np.array([], dtype=np.bool)

    cross_validator = KFold(n_splits=10)
    for train, test in cross_validator.split(X):
        # 教師データを t-SNE で次元縮約する
        X_transformed = manifolder.fit_transform(X)

        X_train, X_test = X_transformed[train], X_transformed[test]
        y_train, y_test = y[train], y[test]

        # 縮約した教師データを学習する
        cls = RandomForestClassifier()
        cls.fit(X_train, y_train)

        y_pred = cls.predict(X_test)
        scores = np.hstack((scores, y_test == y_pred))

    accuracy_score = sum(scores) / len(scores)
    print(accuracy_score)


if __name__ == '__main__':
    main()

実行結果は次の通り。今度は精度が約 97% に向上した。

$ python randomforesttsne.py 
0.973288814691

素のデータセットをそのまま渡す場合に比べると 4% も認識精度が良くなっている。

t-SNE の高速化

ところで、実際に scikit-learn の t-SNE を使うコードを実行してみると、かなり遅いことに気づくはず。どうやら、元々 t-SNE は他の多様体学習アルゴリズムに比べると計算量が多いようだ。ただ、正直このままだと実際のデータセットに使うのは厳しいなあと感じた。そこで、もうちょっと高速に動作する実装がないか調べたところ Multicore-TSNE という実装があった。

次はこれを試してみよう。まずはパッケージをインストールする。

$ pip install MulticoreTSNE

次のサンプルコードでは t-SNE の実装を scikit-learn から Multicore-TSNE に切り替えている。やっていることは scikit-learn 版と変わらない。コード上の変更点もインポート文を変えたのとジョブ数を指定しているくらい。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import multiprocessing

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from MulticoreTSNE import MulticoreTSNE as TSNE

def main():

    dataset = datasets.load_digits()

    X = dataset.data
    y = dataset.target

    manifolder = TSNE(n_jobs=multiprocessing.cpu_count())

    scores = np.array([], dtype=np.bool)

    cross_validator = KFold(n_splits=10)
    for train, test in cross_validator.split(X):
        X_transformed = manifolder.fit_transform(X)

        X_train, X_test = X_transformed[train], X_transformed[test]
        y_train, y_test = y[train], y[test]

        cls = RandomForestClassifier()
        cls.fit(X_train, y_train)

        y_pred = cls.predict(X_test)
        scores = np.hstack((scores, y_test == y_pred))

    accuracy_score = sum(scores) / len(scores)
    print(accuracy_score)


if __name__ == '__main__':
    main()

上記の実行時間は次の通り。今回使った環境では、だいたい 1 分ほどで終わった。

$ time python multicoretsne.py
0.9816360601
python multicoretsne.py  59.58s user 1.51s system 95% cpu 1:03.96 total

比較として scikit-learn 版の実行時間も示しておく。こちらは、なんと 6 分ほどかかっている。

$ time python randomforesttsne.py 
0.979410127991
python randomforesttsne.py  382.42s user 34.13s system 96% cpu 7:11.93 total

64 次元 1797 点で 1 分かあ、と思うところはあるものの 6 倍速いという結果は頼もしい限り。

まとめ

今回は多様体学習アルゴリズムを使ってデータセットの次元を縮約してみた。多様体学習を使って次元を縮約することで、データセットを可視化できたりモデルの認識精度を向上できる場合がある。

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ

作者: もみじあめ
発売日: 2016/03/12
メディア: Kindle版
この商品を含むブログ (1件) を見る

CUBE SUGAR CONTAINER

技術系のこと書きます。

Python: 多様体学習 (Manifold Learning) を用いた次元縮約

下準備

多様体学習を使ってデータセットの次元を縮約する

次元を縮約した結果を教師データとして用いる

t-SNE の高速化

まとめ