Python: 機械学習で分類問題のモデルを評価する指標について

今回は、機械学習において分類問題のモデルを評価するときに使われる色々な指標について扱う。一般的な評価指標としては正確度 (Accuracy) が使われることが多いけど、これには問題も多い。また、それぞれの指標は特徴が異なることから、対象とする問題ごとに重視するものを使い分ける必要がある。

今回扱う代表的な評価指標は次の通り。

正確度 (正解率、Accuracy)
適合率 (精度、陽性反応的中度、Precision)
再現率 (感度、真陽性率、Recall)
F-値 (F-score, F-measure)
AUC (Area Under the Curve)

上記それぞれの指標について、特徴を解説すると共に Python を使って計算してみる。データセットには scikit-learn に組み込みの乳がんデータセットを用いた。今回は「機械学習で」と書いてしまったけど、上記は実際には医療統計の分野でもよく使われる指標だったりする。

尚、今回使った環境は次の通り。

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.12.6
BuildVersion:   16G1114
$ python --version
Python 3.6.3

もくじ
下準備
評価指標を計算する
正確度 (正解率、Accuracy)
適合率 (精度、陽性反応的中度、Precision)
再現率 (感度、真陽性率、Recall)
適合率と再現率のトレードオフについて
適合率と再現率の調整について
F-値 (F-score, F-measure)
AUC (Area Under the Curve)
まとめ

下準備

まずは Python で計算するために必要な準備をする。しばらく地味な作業が続くため、興味がない人は次のセクションまで飛ばしてもらっても良いかも。

最初に、必要なパッケージをインストールしておこう。

$ pip install numpy scipy scikit-learn matplotlib

続いて Python の REPL を起動する。

$ python

そして、乳がんデータセットをロードしておく。

>>> from sklearn import datasets
>>> breast_cancer = datasets.load_breast_cancer()

この乳がんデータセットには、腫瘍について 30 項目のファクターが特徴量として収められている。

>>> breast_cancer.feature_names
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
       'mean smoothness', 'mean compactness', 'mean concavity',
       'mean concave points', 'mean symmetry', 'mean fractal dimension',
       'radius error', 'texture error', 'perimeter error', 'area error',
       'smoothness error', 'compactness error', 'concavity error',
       'concave points error', 'symmetry error', 'fractal dimension error',
       'worst radius', 'worst texture', 'worst perimeter', 'worst area',
       'worst smoothness', 'worst compactness', 'worst concavity',
       'worst concave points', 'worst symmetry', 'worst fractal dimension'],
      dtype='<U23')
>>> len(breast_cancer.feature_names)
30

そして、その腫瘍が悪性 (malignant) か良性 (benign) かラベル付けされている。

>>> breast_cancer.target_names
array(['malignant', 'benign'],
      dtype='<U9')

データセットの説明が済んだところで、特徴量とラベルを取り出しておく。

>>> X, y =  breast_cancer.data, breast_cancer.target

続いては教師データを学習用とテスト用に分割しておく。学習用のデータで評価指標を測ってしまうと、それは汎化性能を表さないため。汎化性能というのは、未知のデータに対するモデルの対処能力のことを指す。

>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)

ここらへんは交差検証や交差検定、とかで調べると色々分かる。

今回は分類器のモデルとしてランダムフォレストを用いた。特にチューニングなどはせず、そのまま使う。

>>> from sklearn.ensemble import RandomForestClassifier
>>> clf = RandomForestClassifier()

ランダムフォレストを学習用のデータを使って学習する。

>>> clf.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
            max_depth=None, max_features='auto', max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
            oob_score=False, random_state=None, verbose=0,
            warm_start=False)

続いてテスト用データを使って推定する。

>>> y_pred = clf.predict(X_test)

ここまでで評価指標を紹介するための準備が整った。

評価指標を計算する

続いて、先ほどのセクションで得られた y_pred と y_test を使って評価指標を計算していく。補足しておくと y_pred はモデルが推定した値で y_test は真の値になっている。

まずは、評価指標を説明する上で必要な定義について確認しておく。説明の中では、モデルの判定結果を 4 種類に分けて扱う。具体的には、次のようなマトリックスで表すことができる。このマトリックスは混同行列 (Confusion Matrix) と呼ばれる。横軸は事実を、縦軸はモデルや検査の推定を表している。

	悪性	良性
陽性	TP	FP
陰性	FN	TN

セルに入った英字は、それぞれ以下のような意味がある。

TP: True Positive
- 正しく陽性と判定できた場合
TN: True Negative
- 正しく陰性と判定できた場合
FP: False Positive
- 本来は陰性なところを、誤って陽性と判定してしまった場合
FN: False Negative
- 本来は陽性なところを、誤って陰性と判定してしまった場合

scikit-learn で混同行列を計算するときは confusion_matrix() 関数が使える。

>>> from sklearn.metrics import confusion_matrix
>>> confusion_matrix(y_test, y_pred)
array([[118,   1],
       [ 45, 121]])

正確度 (正解率、Accuracy)

まずは評価指標として最も一般的な正確度 (Accuracy) から紹介していく。これは、ようするに推定した値と真の値が一致した割合になる。

正確度が使われる場面では FP と FN の重要度について特に考慮しなくても良い場合が考えられる。ちなみに、今回のケースでは FP と FN の重要度は、あきらかに異なる。なぜなら、本当は悪性の患者を良性と判断してしまう (FN) のは患者にとって文字通り致命的なため。このような場面では、正確度だけを見てモデルの良し悪しを判断することはできない。

また、正確度だけ見ているとデータセットの性質によってはモデルを正しく評価するのが難しいケースもある。これは、具体的には陽性と陰性の出現する割合が極端に異なる場合が挙げられる。例えば、医療統計の分野では実際に病気の人は健康な人に比べるとずっと少ないことがよくある。そのような場合、数の多い健康な人をとりあえず健康だと判断しているだけでも正確度は高く出てしまう。これではモデルの良し悪しを正しく評価することは難しい。

正確度の定義は次の通り。

$Accuracy = \frac{TP + TN}{TP + FP + FN + TN}$

定義通りに計算しても良いけど scikit-learn に専用の関数が用意されているので使う。

>>> from sklearn.metrics import accuracy_score
>>> accuracy_score(y_test, y_pred)
0.93333333333333335

このように、評価指標としてよく使われる正確度だけど、実際の運用では適用が難しいケースも多いことが分かった。

適合率 (精度、陽性反応的中度、Precision)

続いて紹介する評価指標は適合率 (Precision) というもの。これは、モデルが陽性と判断したものの中に、どれだけ本当に陽性なものが含まれていたかを示す指標になる。いわば正確性を見るための指標といえる。今回のケースであれば、モデルが悪性と判断したものの中にどれだけ本当に悪性のものが含まれていたか。後述する再現率とはトレードオフの関係にある。

この評価指標は、あきらかに陽性と分かりやすいものだけを見つけたいときに重視するものと考えられる。この評価指標を重視すると、分かりにくいものは基本的に陰性と判断することになる。当然ながら、その中には実際には陽性だったものがたくさん含まれているはず。つまり、適合率を重視するときは FN が発生することが許容できるケースといえる。それでもなお FP があっては困るときに適合率を使うことができる。

今回のケースでいうと、この評価指標を重視すべきでないことはあきらかだ。 FN が発生した場合、それは患者の生命に関わる。

定義は次の通り。

$Precision = \frac{TP}{TP + FP}$

定義通りに計算しても良いけど、先ほどと同じように専用の関数を使ってしまうのが楽ちん。

>>> from sklearn.metrics import precision_score
>>> precision_score(y_test, y_pred)
0.95402298850574707

再現率 (感度、真陽性率、Recall)

続いて紹介するのは再現率 (Recall) という評価指標になる。これは、実際に陽性だったもののうちモデルが陽性と判断したものの割合を指す。いわば網羅性を見るための指標といえる。今回のケースであれば本当に悪性だったものの中でモデルが悪性と判断できたものの割合になる。先述した適合率とはトレードオフの関係にある。

この評価指標は、怪しいものはとりあえず全て見つけ出したいときに重視すべきものと考えられる。この評価指標を重視すると、分かりにくいものは基本的に陽性と判断することになる。当然ながら、その中には実際には陰性だったものがたくさん含まれているはず。つまり、再現率を重視するときは FP が発生することが許容できるケースといえる。それでもなお FN があっては困るときに再現率を使うことができる。

今回のケースでいうと、この評価指標を重視するのが適当とかんがえられる。 FP は、再検査などを受けて実際には陰性と分かったとき「よかったですね」で済む。もちろん無いに越したことはないものの FN が発生することに比べれば、ずっと重要度は低い。

定義は次の通り。

$Recall = \frac{TP}{TP + FN}$

これについても scikit-learn に計算用の関数が用意されている。

>>> from sklearn.metrics import recall_score
>>> recall_score(y_test, y_pred)
0.93785310734463279

適合率と再現率のトレードオフについて

前述した通り、適合率と再現率はトレードオフの関係にある。ここでは、それについて単純化した例を使って説明したい。

まずは次の図を見てほしい。これは、ある因子が取る値によって疾病の有無の確率が変化することを示したグラフになっている。例えば血液検査して得られた特定の項目が高いと、ある疾病を持っている確率が高い、みたいな感じ。もちろん、これは説明するために用意したものなので実際にこのような関係になっているものが具体的にあるわけではない。

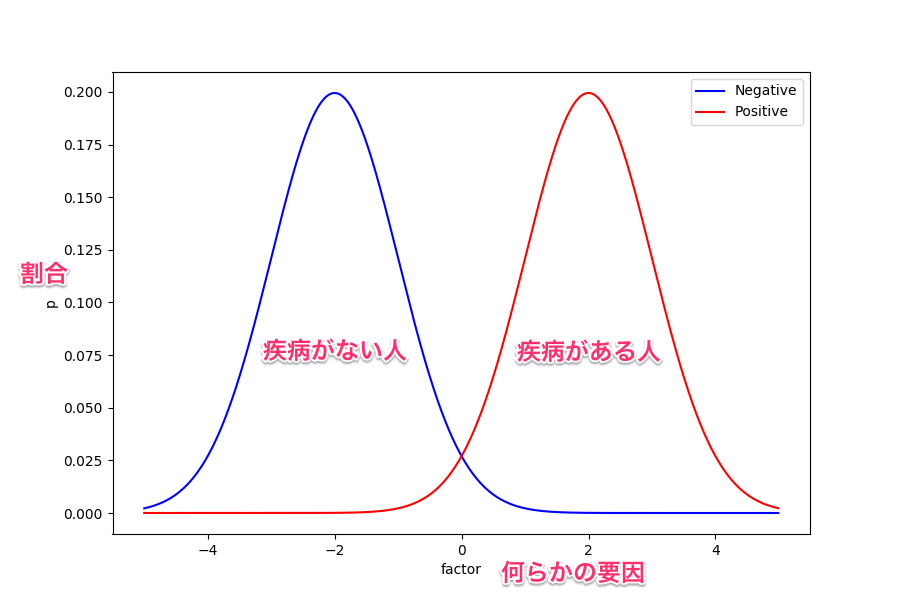
f:id:momijiame:20171218003752p:plain

ここで、要因は一つしかないので横軸の何処かに識別境界を置いて疾病の有無を判断することになる。ようするに、この閾値より上であれば疾病ありと判断、下であれば疾病なしと判断するというわけ。

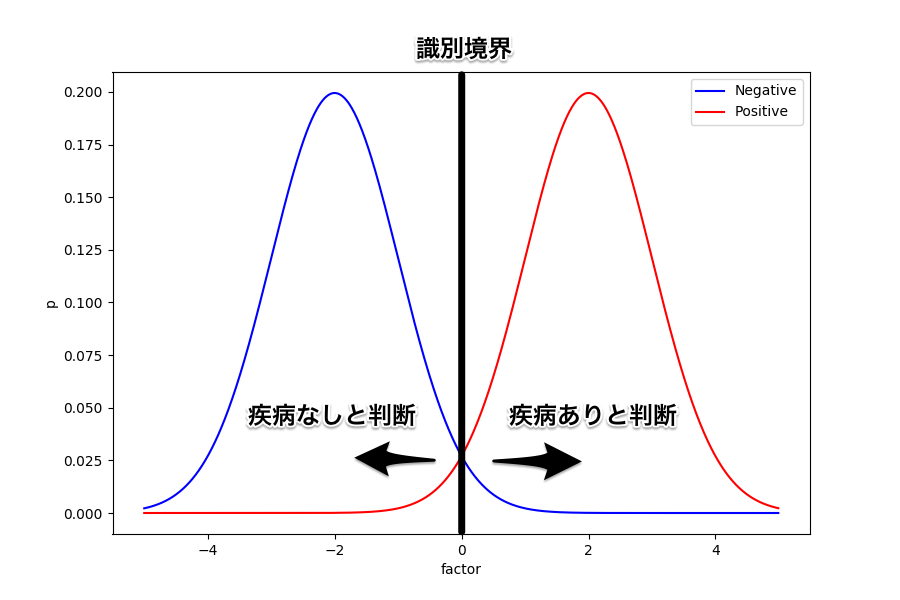
f:id:momijiame:20171218003809p:plain

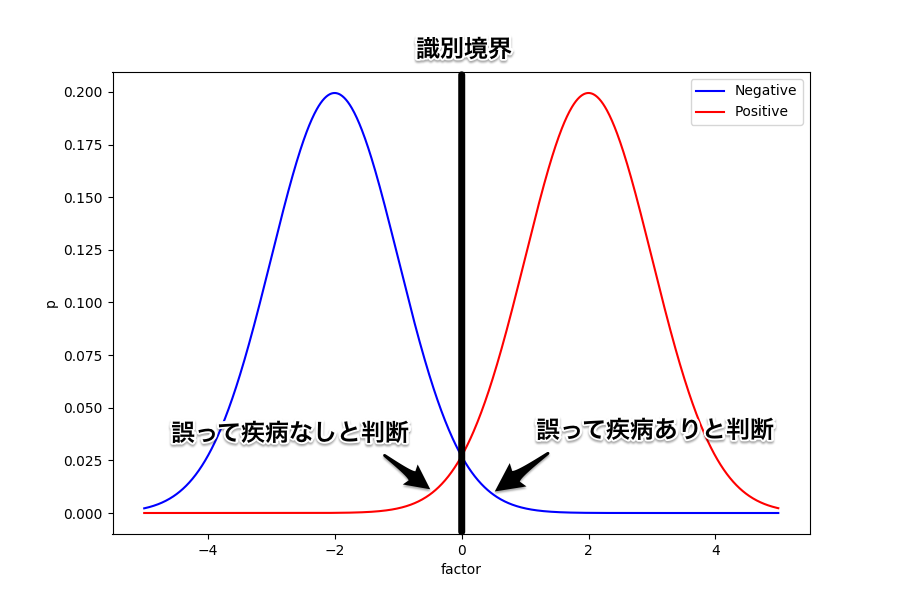
例えば識別境界をど真ん中に置いてみたときはどうなるだろう。誤って疾病あり (FP) と判断される人と誤って疾病なし (FN) と判断される人が同じように出ることになる。

f:id:momijiame:20171218003819p:plain

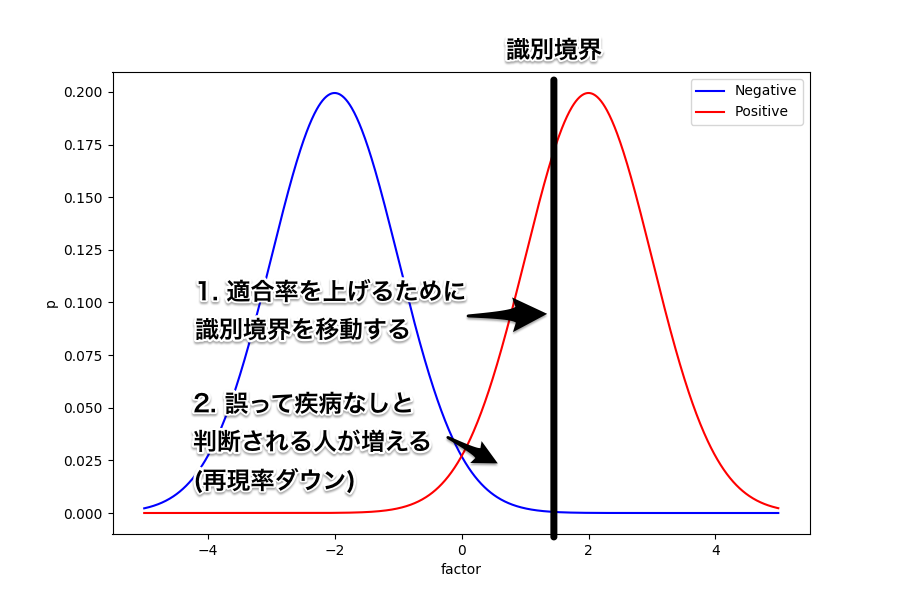
続いては、識別境界を右にずらしてみよう。このときは、誤って疾病あり (FP) と判断される人は減るため適合率は上がることになる。しかし、反対に誤って疾病なし (FN) と判断される人は増えることから再現率は下がってしまう。

f:id:momijiame:20171218003837p:plain

同じように、識別境界を今度は左にずらしてみよう。すると、誤って疾病なし (FN) と判断される人は減るため再現率は上がる。反対に、誤って疾病あり (FP) と判断される人は増えるので適合率は下がってしまうことが分かる。

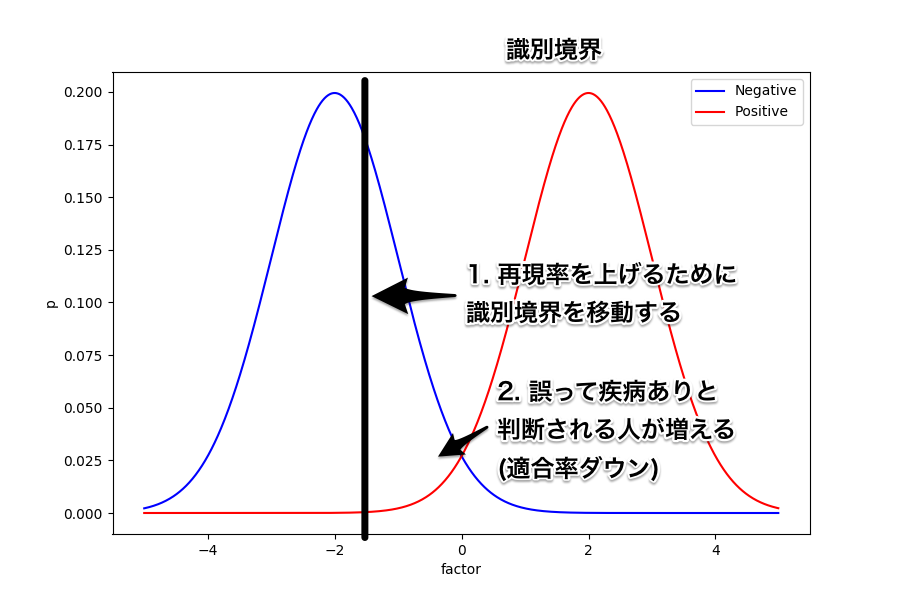
f:id:momijiame:20171218003845p:plain

このように、単純化した例を使うと両者がトレードオフの関係にあることが分かりやすい。

適合率と再現率の調整について

続いては、実際に scikit-learn を使って適合率と再現率を調整してみよう。

元々の predict() メソッドでは閾値を 0.5 にしてある。

>>> clf.predict(X_test)
array([1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0,
       0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0,
       1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1,
       1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1,
       1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0,
       1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
       1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0,
       1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1,
       1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0,
       1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1,
       1, 0, 1, 1, 1, 1, 0, 1, 1])

一体何が 0.5 なのかというと、そのクラスに分類される閾値のこと。 predict_proba() メソッドを使うと、そのクラスに分類される確率が得られる。例えば 4 番目の項目はクラス 0 に分類される確率が 0.6 でクラス 1 に分類される確率が 0.4 だった。閾値が 0.5 にあるとき、この項目はクラス 0 に分類されることになる。

>>> clf.predict_proba(X_test)
array([[ 0. ,  1. ],
       [ 0.1,  0.9],
       [ 1. ,  0. ],
       [ 0.6,  0.4],
...(snip)...
       [ 0.9,  0.1],
       [ 0. ,  1. ],
       [ 0. ,  1. ]])

次のようにすると、自分で閾値を変更した分類結果が得られる。

>>> (clf.predict_proba(X_test)[:, 0] < 0.5).astype(int)
array([1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0,
       0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0,
       1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1,
       1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1,
       1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0,
       1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
       1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0,
       1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1,
       1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0,
       1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1,
       1, 0, 1, 1, 1, 1, 0, 1, 1])

実際に閾値をずらしながら評価指標が変化することを確認してみよう。まずは閾値を変えることで再現率を上げてみる。

>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.5).astype(int)
>>> recall_score(y_test, y_pred)
0.96385542168674698
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.6).astype(int)
>>> recall_score(y_test, y_pred)
0.98795180722891562
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.7).astype(int)
>>> recall_score(y_test, y_pred)
0.99397590361445787
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.8).astype(int)
>>> recall_score(y_test, y_pred)
1.0

閾値を反対に変化させれば適合率を上げることができる。

>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.5).astype(int)
>>> precision_score(y_test, y_pred)
0.97560975609756095
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.4).astype(int)
>>> precision_score(y_test, y_pred)
0.97530864197530864
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.3).astype(int)
>>> precision_score(y_test, y_pred)
0.98709677419354835
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.2).astype(int)
>>> precision_score(y_test, y_pred)
0.99305555555555558
>>> y_pred = (clf.predict_proba(X_test)[:, 0] < 0.1).astype(int)
>>> precision_score(y_test, y_pred)
0.99180327868852458

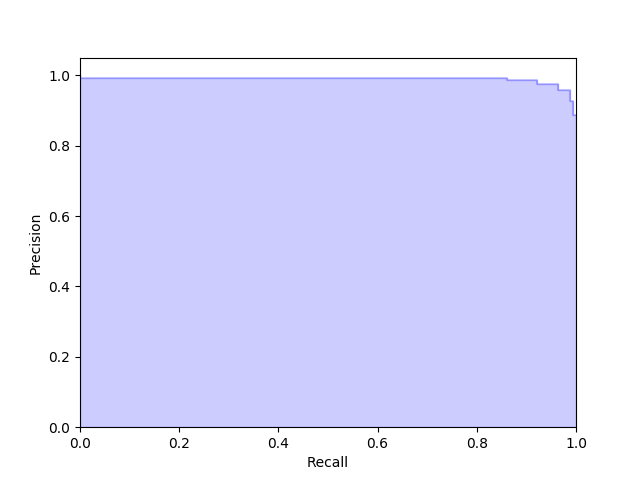
また、次のように precision_recall_curve() 関数を使うと両者の関係をグラフ化できる。

>>> from sklearn.metrics import precision_recall_curve
>>> precision, recall, thresholds = precision_recall_curve(y_test, clf.predict_proba(X_test)[:, 1])
>>> plt.step(recall, precision, color='b', alpha=0.2,
...          where='post')
[<matplotlib.lines.Line2D object at 0x1189cac18>]
>>> plt.fill_between(recall, precision, step='post', alpha=0.2,
...                  color='b')
<matplotlib.collections.PolyCollection object at 0x1189cadd8>
>>>
>>> plt.xlabel('Recall')
Text(0.5,0,'Recall')
>>> plt.ylabel('Precision')
Text(0,0.5,'Precision')
>>> plt.ylim([0.0, 1.05])
(0.0, 1.05)
>>> plt.xlim([0.0, 1.0])
(0.0, 1.0)
>>> plt.show()

今回のモデルであれば次のようなグラフが得られた。

f:id:momijiame:20171218003905p:plain

F-値 (F-score, F-measure)

続いて紹介する評価指標は、F-値 (F-score, F-measure) というもの。これは、先述した適合率と再現率の調和平均を取ったものになっている。両者のバランスが極端に悪くないものを作りたいときは、この評価指標を使うのが良いようだ。

正確度では陽性と陰性の出現する割合が極端に異なると、正しくモデルを評価するのが難しかった。それに対しF-値はそのような場合であっても評価しやすい。そのため、常に正確度ではなくF-値を使って評価することを推奨する人もいるようだ。

定義は次の通り。

$F-measure = 2 \frac{Precision \cdot Recall}{Precision + Recall}$

これも scikit-learn に計算用の関数がある。

>>> from sklearn.metrics import f1_score
>>> f1_score(y_test, y_pred)
0.94586894586894577

AUC (Area Under the Curve)

続いて紹介するのは AUC (Area under the curve) という評価指標になる。ただ、この AUC を理解するには、その前に ROC (Receiver Operating Characteristic) 曲線というものを理解しなきゃいけない。 ROC 曲線は、日本語だと受信者動作特性曲線とも言ったりする。

ROC 曲線というのは、縦軸に再現率を、横軸に特異度をプロットしたグラフのことをいう。特異度という新しい言葉が登場したけど、これは実際に陰性だったもののうちモデルが陰性と判断したものの割合を指す。特異度は、真陰性率とも呼ばれるほか英語では Specificity となる。

特異度の定義は次の通り。

$Specificity = \frac{TN}{TN + FP}$

上記、再現率と特異度の関係を二次元でグラフ化したものが ROC 曲線と呼ばれる。

実際に今回のモデルを使って ROC 曲線を描いてみよう。 scikit-learn で ROC 曲線を得るには roc_curve() 関数が使える。

>>> from sklearn.metrics import roc_curve
>>> fpr, tpr, _ = roc_curve(y_test, clf.predict_proba(X_test)[:, 1])
>>> plt.step(fpr, tpr, color='b', alpha=0.2, where='post')
[<matplotlib.lines.Line2D object at 0x131100cc0>]
>>> plt.fill_between(fpr, tpr, step='post', alpha=0.2, color='b')
<matplotlib.collections.PolyCollection object at 0x12b7b22b0>
>>> plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
[<matplotlib.lines.Line2D object at 0x12b7b2160>]
>>> plt.ylabel('True Positive Rate')
Text(0,0.5,'True Positive Rate')
>>> plt.xlabel('False Positive Rate')
Text(0.5,0,'False Positive Rate')
>>> plt.ylim([0.0, 1.0])
(0.0, 1.0)
>>> plt.xlim([0.0, 1.0])
(0.0, 1.0)
>>> plt.show()

上記で得られたグラフが次の通り。

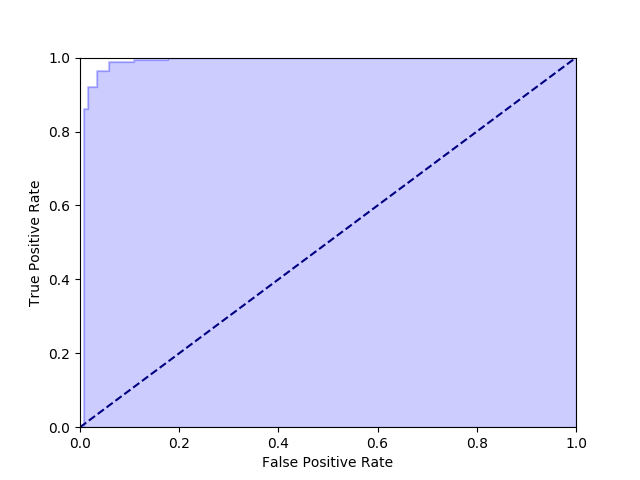
f:id:momijiame:20171218003922p:plain

ROC 曲線では、上記の青い部分が多いほど (白い部分が少ないほど) 優れたモデルということを表している。そして、その優れたモデルかどうかを表す評価指標が実は AUC ということになる。 AUC というのは、ようするに青い部分の面積を 0.5 ~ 1 の間で表現したものだ。

どうして 0.5 以上になるかというと、それは ROC 曲線の特性とも関わってくる。 ROC 曲線に斜めの破線が描かれていたことに気づいただろうか。実は、二値分類を完全にランダムに実行すると、ROC 曲線はこの斜めの破線上に存在して AUC も 0.5 になる。もし、ROC 曲線が斜めの破線より下にあって AUC が 0.5 未満ということは、つまりランダムに分類するよりも性能が悪いことになる。その場合だと、予測内容を反転してしまった方がマシということだ。つまり AUC は 0.5 以上でないとおかしい。

scikit-learn で AUC を計算するには auc() 関数が使える。先ほど計算した再現率と特異度を渡してやろう。

>>> from sklearn.metrics import auc
>>> auc(fpr, tpr)
0.99141945935000508

まとめ

今回は、機械学習において分類問題のモデルを評価するときに使われる色々な指標を紹介した。評価指標はそれぞれ特性が異なるため、問題に応じて適材適所で使い分ける必要がある。

はじめてのパターン認識

作者:平井有三
森北出版

Amazon

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ

作者:もみじあめ

Amazon

CUBE SUGAR CONTAINER

技術系のこと書きます。

Python: 機械学習で分類問題のモデルを評価する指標について

もくじ

下準備

評価指標を計算する

正確度 (正解率、Accuracy)

適合率 (精度、陽性反応的中度、Precision)

再現率 (感度、真陽性率、Recall)

適合率と再現率のトレードオフについて

適合率と再現率の調整について

F-値 (F-score, F-measure)

AUC (Area Under the Curve)

まとめ