k 近傍法 (k-Nearest Neighbor algorithm) というのは、機械学習において教師あり学習で分類問題を解くためのアルゴリズム。 教師あり学習における分類問題というのは、あらかじめ教師信号として特徴ベクトルと正解ラベルが与えられるものをいう。 その教師信号を元に、未知の特徴ベクトルが与えられたときに正解ラベルを予想しましょう、というもの。
k 近傍法は機械学習アルゴリズムの中でも特にシンプルな実装になっている。 じゃあ、シンプルな分だけ性能が悪いかというと、そんなことはない。 分類精度であれば、他のアルゴリズムに比べても引けを取らないと言われている。 ただし、計算量が多いという重大な欠点がある。 そのため、それを軽減するための改良アルゴリズムも数多く提案されている。
k 近傍法では、与えられた未知の特徴ベクトルを、近い場所にある教師信号の正解ラベルを使って分類する。 特徴ベクトルで近くにあるものは似たような性質を持っているはず、という考え方になっている。 今回は、そんな k 近傍法の基本的な実装を Python で書いてみることにした。
使った環境は次の通り。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.12.3 BuildVersion: 16D32 $ python --version Python 3.5.3
依存パッケージをインストールする
あらかじめ、今回のソースコードで使う依存パッケージをインストールしておく。
$ pip install numpy scipy scikit-learn
最近傍法を実装してみる
k 近傍法では、未知の特徴ベクトルの近くにある k 点の教師信号を用いる。 この k 点を 1 にしたときのことを特に最近傍法 (Nearest Neighbor algorithm) と呼ぶ。 一番近い場所にある教師信号の正解ラベルを返すだけなので、さらに実装しやすい。 そこで、まずは最近傍法から書いてみることにしよう。
次のサンプルコードでは最近傍法を NearestNeighbors というクラスで実装している。
インターフェースは scikit-learn っぽくしてみた。
分類するデータセットは Iris (あやめ) を使っている。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from sklearn import datasets from sklearn.model_selection import LeaveOneOut from sklearn.metrics import accuracy_score class NearestNeighbors(object): def __init__(self): self._train_data = None self._target_data = None def fit(self, train_data, target_data): """訓練データを学習する""" # あらかじめ計算しておけるものが特にないので保存だけする self._train_data = train_data self._target_data = target_data def predict(self, x): """訓練データから予測する""" # 判別する点と教師データとのユークリッド距離を計算する distances = np.array([self._distance(p, x) for p in self._train_data]) # 最もユークリッド距離の近い要素のインデックスを得る nearest_index = distances.argmin() # 最も近い要素のラベルを返す return self._target_data[nearest_index] def _distance(self, p0, p1): """二点間のユークリッド距離を計算する""" return np.sum((p0 - p1) ** 2) def main(): # Iris データセットをロードする iris_dataset = datasets.load_iris() # 特徴データとラベルデータを取り出す features = iris_dataset.data targets = iris_dataset.target # LOO 法で汎化性能を調べる predicted_labels = [] loo = LeaveOneOut() for train, test in loo.split(features): train_data = features[train] target_data = targets[train] # モデルを学習させる model = NearestNeighbors() model.fit(train_data, target_data) # 一つ抜いたテストデータを識別させる predicted_label = model.predict(features[test]) predicted_labels.append(predicted_label) # 正解率を出力する score = accuracy_score(targets, predicted_labels) print(score) if __name__ == '__main__': main()
上記のサンプルコードでは Leave-One-Out 法というやり方で交差検証をしている。
交差検証というのは、学習に使わなかったデータを使って正解を導くことができたか調べる方法を指す。 モデルの性能は、未知のデータに対する対処能力で比べる必要がある。 この、未知のデータに対する対処能力のことを汎化性能と呼ぶ。 交差検証をすることで、この汎化性能を測ることができる。
Leave-One-Out 法では、教師信号の中から検証用のデータをあらかじめ一つだけ抜き出しておく。 そして、それをモデルが正解できるのか調べるやり方だ。 抜き出す対象を一つずつずらしながら、データセットに含まれる要素の数だけ繰り返す。 他の交差検証に比べると計算量は増えるものの、厳密で分かりやすい。
上記のサンプルコードの実行結果は次の通り。
$ python nn.py
0.96
汎化性能で 96% の正解率が得られた。
scikit-learn を使う場合
ちなみに、自分で書く代わりに scikit-learn にある実装を使う場合も紹介しておく。
次のサンプルコードは k 近傍法の実装を scikit-learn の KNeighborsClassifier に代えたもの。
インターフェースを揃えてあったので、使うクラスが違う以外は先ほどと同じソースコードになっている。
scikit-learn で最近傍法をしたいときは KNeighborsClassifier の k に 1 を指定するだけで良い。
#!/usr/bin/env python # -*- coding: utf-8 -*- from sklearn import datasets from sklearn.model_selection import LeaveOneOut from sklearn.metrics import accuracy_score from sklearn.neighbors import KNeighborsClassifier def main(): iris_dataset = datasets.load_iris() features = iris_dataset.data targets = iris_dataset.target predicted_labels = [] loo = LeaveOneOut() for train, test in loo.split(features): train_data = features[train] target_data = targets[train] model = KNeighborsClassifier(n_neighbors=1) model.fit(train_data, target_data) predicted_label = model.predict(features[test]) predicted_labels.append(predicted_label) score = accuracy_score(targets, predicted_labels) print(score) if __name__ == '__main__': main()
上記のサンプルコードの実行結果は次の通り。
$ python knn_scikit.py
0.96
当然だけど同じ班化性能になっている。
k 近傍法を実装してみる
先ほど示した最近傍法の実装では、最寄りの教師信号だけを使うものとなっていた。 今度は、より汎用的に近くにある k 点の教師信号を使う実装にしてみる。
次のサンプルコードでは KNearestNeighbors クラスのコンストラクタに k を渡せるようになっている。
実装としては、分類するときに教師信号をユークリッド距離でソートした上で k 個を取り出している。
ひとまず k については 3 を指定した。
もしこれを 1 にすれば最近傍法になる。
#!/usr/bin/env python # -*- coding: utf-8 -*- from collections import Counter import numpy as np from sklearn import datasets from sklearn.model_selection import LeaveOneOut from sklearn.metrics import accuracy_score class KNearestNeighbors(object): def __init__(self, k=1): self._train_data = None self._target_data = None self._k = k def fit(self, train_data, target_data): """訓練データを学習する""" # あらかじめ計算しておけるものが特にないので保存だけする self._train_data = train_data self._target_data = target_data def predict(self, x): """訓練データから予測する""" # 判別する点と教師データとのユークリッド距離を計算する distances = np.array([self._distance(p, x) for p in self._train_data]) # ユークリッド距離の近い順でソートしたインデックスを得る nearest_indexes = distances.argsort()[:self._k] # 最も近い要素のラベルを返す nearest_labels = self._target_data[nearest_indexes] # 近傍のラベルで一番多いものを予測結果として返す c = Counter(nearest_labels) return c.most_common(1)[0][0] def _distance(self, p0, p1): """二点間のユークリッド距離を計算する""" return np.sum((p0 - p1) ** 2) def main(): iris_dataset = datasets.load_iris() features = iris_dataset.data targets = iris_dataset.target predicted_labels = [] loo = LeaveOneOut() for train, test in loo.split(features): train_data = features[train] target_data = targets[train] model = KNearestNeighbors(k=3) model.fit(train_data, target_data) predicted_label = model.predict(features[test]) predicted_labels.append(predicted_label) score = accuracy_score(targets, predicted_labels) print(score) if __name__ == '__main__': main()
上記の実行結果は次の通り。
$ python knn.py
0.96
汎化性能は k=1 のときと変わらないようだ。
最適な k を探す
k 近傍法では、計算に近傍何点を使うか (ようするに k) がハイパーパラメータとなっている。 ハイパーパラメータというのは、機械学習において人間が調整する必要のあるパラメータのことをいう。
次は、最適な k を探してみることにする。 といっても、やることは単に総当りで探すだけ。
せっかくならパラメータによる汎化性能の違いを可視化したい。 そこで matplotlib も入れておこう。
$ pip install matplotlib $ mkdir -p ~/.matplotlib $ cat << 'EOF' > ~/.matplotlib/matplotlibrc backend: TkAgg EOF
次のサンプルコードでは k を 1 ~ 20 の間で調整しながら総当りで汎化性能を計算している。 データセットごとに最適な k が異なるところを見ておきたいので Iris (あやめ) と Digits (数字) で調べることにした。 自分で実行するときは、データセットのロード部分にあるコメントアウトを切り替えてほしい。
#!/usr/bin/env python # -*- coding: utf-8 -*- from matplotlib import pyplot as plt from sklearn import datasets from sklearn.model_selection import LeaveOneOut from sklearn.metrics import accuracy_score from sklearn.neighbors import KNeighborsClassifier def main(): # データセットをロードする dataset = datasets.load_digits() # dataset = datasets.load_iris() # 特徴データとラベルデータを取り出す features = dataset.data targets = dataset.target # 検証する近傍数の上限 K = 20 ks = range(1, K + 1) # 使う近傍数ごとに正解率を計算する accuracy_scores = [] for k in ks: # Leave-One-Out 法で汎化性能を測る predicted_labels = [] loo = LeaveOneOut() for train, test in loo.split(features): train_data = features[train] target_data = targets[train] # モデルを学習させる model = KNeighborsClassifier(n_neighbors=k) model.fit(train_data, target_data) # 一つだけ取り除いたテストデータを識別させる predicted_label = model.predict(features[test]) predicted_labels.append(predicted_label) # 正解率を計算する score = accuracy_score(targets, predicted_labels) print('k={0}: {1}'.format(k, score)) accuracy_scores.append(score) # 使う近傍数ごとの正解率を折れ線グラフで可視化する X = list(ks) plt.plot(X, accuracy_scores) plt.xlabel('k') plt.ylabel('accuracy rate') plt.show() if __name__ == '__main__': main()
まずはデータセットとして Digits を使ったときから。 実行結果は次のようになる。
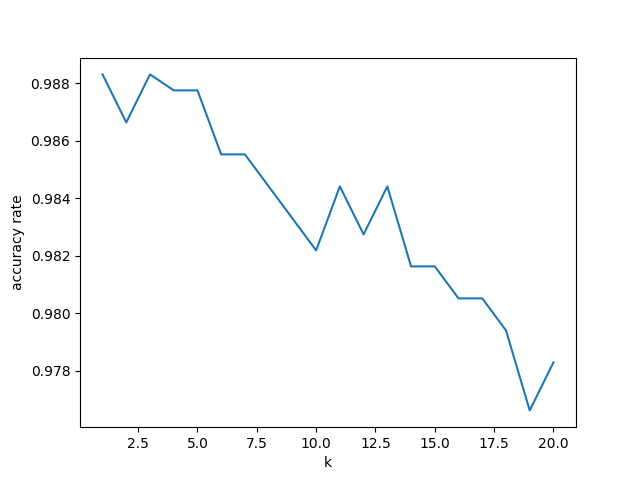
$ python knn_tuning.py k=1: 0.988313856427379 k=2: 0.986644407345576 k=3: 0.988313856427379 k=4: 0.9877573734001113 k=5: 0.9877573734001113 k=6: 0.9855314412910406 k=7: 0.9855314412910406 k=8: 0.9844184752365053 k=9: 0.9833055091819699 k=10: 0.9821925431274346 k=11: 0.9844184752365053 k=12: 0.9827490261547023 k=13: 0.9844184752365053 k=14: 0.9816360601001669 k=15: 0.9816360601001669 k=16: 0.9805230940456316 k=17: 0.9805230940456316 k=18: 0.9794101279910963 k=19: 0.9766277128547579 k=20: 0.9782971619365609
どうやら Digits のときは k を 1 か 3 にするのが良さそうだ。
続いて Iris を使ったとき。
$ python knn_tuning.py k=1: 0.96 k=2: 0.9466666666666667 k=3: 0.96 k=4: 0.96 k=5: 0.9666666666666667 k=6: 0.96 k=7: 0.9666666666666667 k=8: 0.9666666666666667 k=9: 0.9666666666666667 k=10: 0.9733333333333334 k=11: 0.9733333333333334 k=12: 0.96 k=13: 0.9666666666666667 k=14: 0.9733333333333334 k=15: 0.9733333333333334 k=16: 0.9666666666666667 k=17: 0.9733333333333334 k=18: 0.9733333333333334 k=19: 0.98 k=20: 0.98
今度は全然違うグラフになった。
どうやら Iris なら k は 20 にするのが良いらしい。
もしかすると、さらに増やすと良い可能性もある?

まとめ
今回は Python を使って教師あり学習の分類問題を解くためのアルゴリズムの一つ、k 近傍法を実装してみた。 k 近傍法は単純な割に分類精度は決して低くないものの、計算量が多いという欠点がある。 k 近傍法では、計算に近傍何点を使うのが適しているかはデータセットによって異なる。 そのため、異なる k を使って汎化性能を測定して決定しよう。
ちなみに、計算量の多さを軽減するための手法としては、圧縮型 k 近傍法、分岐限定法、疑似最近傍探索などがあるようだ。 それらについては、機会があれば改めて実装してみたい。

- 作者: 平井有三
- 出版社/メーカー: 森北出版
- 発売日: 2012/07/31
- メディア: 単行本(ソフトカバー)
- 購入: 1人 クリック: 7回
- この商品を含むブログ (3件) を見る

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログ (1件) を見る