Python: statsmodels で時系列データを基本成分に分解する

時系列データを扱うとき、原系列が傾向変動・季節変動・不規則変動という基本成分の合成で成り立っていると捉えることがある。傾向変動は中長期的な増加・減少といった変化であり、季節変動は例えば 1 ヶ月や 1 年といった周期的な変化を指している。不規則変動は、前者 2 つに当てはまらない変化で、誤差変動と特異的変動に分けて考える場合もあるようだ。

原系列が基本成分の合成と考える場合でも、捉え方として加法モデルと乗法モデルにさらに分かれる。まず、加法モデルでは傾向変動 $T(t)$ と季節変動 $S(t)$ 、誤差変動 $I(t)$ の和を原系列 $O(t)$ と捉える。この考え方では、傾向変動の大きさに関係なく一定の季節変動が加えられる。

$O(t) = T(t) + S(t) + I(t)$

一方で、乗法モデルでは積と捉える。つまり、傾向変動が大きくなれば、それに比例して季節変動も大きくなる、という考え方。

$O(t) = T(t) \times S(t) \times I(t)$

これらは扱うデータやタスクによって使い分ける必要があるらしい。今回は、Python の statsmodels を使って原系列を基本成分に分解してみる。

使った環境は次のとおり。

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.14.6
BuildVersion:   18G3020
$ python -V                      
Python 3.7.7

下準備

まずは、必要なパッケージをインストールしておく。

$ pip install statsmodels seaborn

現系列を基本成分に分解する

現系列を基本成分に分解するには seasonal_decompose() 関数を使う。次のサンプルコードでは、旅客機の乗客数のデータを分解してみた。なお、モデルとしては乗法モデルを仮定している。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import pandas as pd
import seaborn as sns
from statsmodels import api as sm
from matplotlib import pyplot as plt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()


def main():
    # 旅客機の乗客数のデータセットを読み込む
    df = sns.load_dataset('flights')

    df['year-month'] = df.month.astype(str) + ', ' + df.year.astype(str)
    df['year-month'] = pd.to_datetime(df['year-month'], format='%B, %Y')
    df = df.set_index('year-month')

    # 時系列データを傾向変動・季節変動・残差に分解する
    decompose_result = sm.tsa.seasonal_decompose(df['passengers'],
                                                 # 乗法モデルを仮定する
                                                 model='multiplicative')

    # これでもグラフが描ける
    # decompose_result.plot()

    # 描画する領域を用意する
    fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(8, 8), sharex=True)

    # 原系列
    axes[0].set_title('Observed')
    axes[0].plot(decompose_result.observed)

    # 傾向変動
    axes[1].set_title('Trend')
    axes[1].plot(decompose_result.trend)

    # 季節変動
    axes[2].set_title('Seasonal')
    axes[2].plot(decompose_result.seasonal)

    # 残差 (不規則変動 = 誤差変動 + 特異的変動)
    axes[3].set_title('Residual')
    axes[3].plot(decompose_result.resid)

    # グラフを表示する
    plt.show()


if __name__ == '__main__':
    main()

上記を実行してみよう。

$ python decompose.py

次のようなグラフが得られる。上から原系列、傾向変動、季節変動、不規則変動 (残差) となっている。

f:id:momijiame:20200406232249p:plain — 原系列を基本成分に分解する

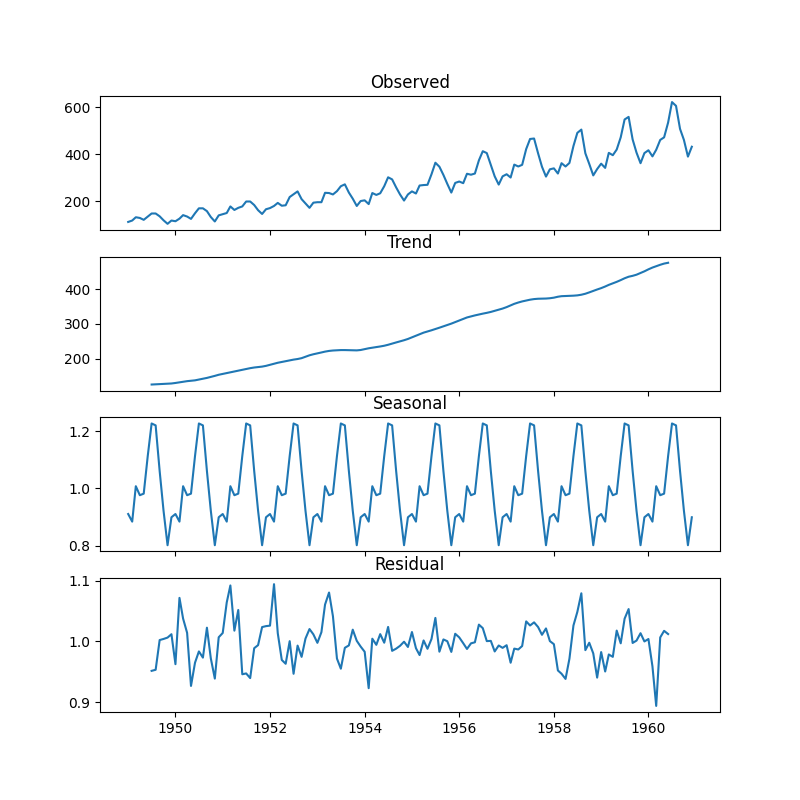
注意すべきポイントとして、seasonal_decompose() 関数では傾向変動と不規則変動は端の要素が NaN になってしまうようだ。

原系列と傾向変動で偏自己相関を見比べてみる

時系列データに周期性、つまり季節成分が含まれるか調べる方法のひとつに、偏自己相関を調べるというのがある。今回は、分解する前の原系列と、分解した後の傾向変動について、自己相関と偏自己相関を調べて見比べてみよう。自己相関では、ある時点のデータ $O(t)$ には 1 つ前のデータ $O(t - 1)$ が関係している可能性がある。そして、1 つ前のデータには、さらにその 1 つ前のデータが、というような積み重ねの影響を受けている恐れがある。偏自己相関は、そのような積み重ねの影響を消去することを目的とした統計量になっている。

次のサンプルコードでは、分解する前の原系列と分解した後の傾向変動について自己相関と偏自己相関を計算してグラフにプロットしている。なお、データに NaN があると自己相関がうまく計算できないようなので、傾向変動からは NaN を除外している。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import pandas as pd
import seaborn as sns
from statsmodels import api as sm
from matplotlib import pyplot as plt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()


def main():
    # 旅客機の乗客数のデータセットを読み込む
    df = sns.load_dataset('flights')

    df['year-month'] = df.month.astype(str) + ', ' + df.year.astype(str)
    df['year-month'] = pd.to_datetime(df['year-month'], format='%B, %Y')
    df = df.set_index('year-month')

    # 時系列データを傾向変動・季節変動・残差に分解する
    decompose_result = sm.tsa.seasonal_decompose(df['passengers'],
                                                 # 乗法モデルを仮定する
                                                 model='multiplicative')

    _, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 8))

    # 原系列の ACF
    sm.tsa.graphics.plot_acf(df['passengers'], ax=axes[0][0])
    # 原系列の PACF
    sm.tsa.graphics.plot_pacf(df['passengers'], ax=axes[1][0])

    # 傾向変動の ACF
    sm.tsa.graphics.plot_acf(decompose_result.trend.dropna(), ax=axes[0][1])
    # 傾向変動の PACF
    sm.tsa.graphics.plot_pacf(decompose_result.trend.dropna(), ax=axes[1][1])

    # グラフを表示する
    plt.show()


if __name__ == '__main__':
    main()