以前から移動平均 (MA: Moving Average) という手法自体は知っていたけど、中心化移動平均 (CMA: Centered Moving Average) というものがあることは知らなかった。 一般的な移動平均である後方移動平均は、データの対応関係が原系列に対して遅れてしまう。 そこで、中心化移動平均という手法を使うことで遅れをなくすらしい。 この手法は、たとえば次のような用途でひとつのやり方として使われているようだ。
- 不規則変動の除去
- 季節変動の除去
使った環境は次のとおり。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.14.6 BuildVersion: 18G3020 $ python -V Python 3.7.7
下準備
下準備として、必要なパッケージをインストールしておく。
$ pip install pandas seaborn
インストールできたら Python のインタプリタを起動する。
$ python
起動できたら、1 ~ 12 までの数字が入った Series のオブジェクトを作る。
>>> import pandas as pd >>> x = pd.Series(range(1, 12 + 1)) >>> x 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 dtype: int64
上記のオブジェクトを使って移動平均の計算方法について学んでいく。
(後方) 移動平均 (MA: Moving Average)
はじめに、一般的な移動平均である後方移動平均から試す。
Pandas では rolling() メソッドを使うことで移動平均を計算できる。
以下では 3 点の要素で平均をとる 3 点移動平均を計算している。
>>> backward_3p_ma = x.rolling(window=3).mean() >>> backward_3p_ma 0 NaN 1 NaN 2 2.0 3 3.0 4 4.0 5 5.0 6 6.0 7 7.0 8 8.0 9 9.0 10 10.0 11 11.0 dtype: float64
この計算では、たとえばインデックスで 2 に入る要素は、次のように計算される。
backward_3p_ma[2] = (x[0] + x[1] + x[2]) / 3
つまり、自分よりも後ろの値を使って平均を計算することになる。
この計算方法では、原系列との対応関係を考えたとき次のように 1 つ分の遅れが出る。
>>> pd.concat([x, backward_3p_ma], axis=1) 0 1 0 1 NaN 1 2 NaN 2 3 2.0 3 4 3.0 4 5 4.0 5 6 5.0 6 7 6.0 7 8 7.0 8 9 8.0 9 10 9.0 10 11 10.0 11 12 11.0
中心化移動平均 (CMA: Centered Moving Average)
そこで、遅れの影響を取り除いたものが中心化移動平均と呼ばれるらしい。
たとえば、平均をとる要素数が奇数のときは、単に rolling() メソッドの center オプションを有効にするだけで良い。
>>> centered_3p_ma = x.rolling(window=3, center=True).mean() >>> centered_3p_ma 0 NaN 1 2.0 2 3.0 3 4.0 4 5.0 5 6.0 6 7.0 7 8.0 8 9.0 9 10.0 10 11.0 11 NaN dtype: float64
このオプションが有効だと、たとえばインデックスで 2 に入る要素は、次のように計算される。
つまり、自分の前後にある値を使って平均を計算することになる。
centered_3p_ma[2] = (x[1] + x[2] + x[3]) / 3
現系列との対応関係を確認すると、このやり方では遅れがなくなっている。
>>> pd.concat([x, centered_3p_ma], axis=1) 0 1 0 1 NaN 1 2 2.0 2 3 3.0 3 4 4.0 4 5 5.0 5 6 6.0 6 7 7.0 7 8 8.0 8 9 9.0 9 10 10.0 10 11 11.0 11 12 NaN
ただし、このオプションは実装的には単に後方移動平均を計算した上で shift() しているだけに過ぎないらしい。
ようするに、こういうこと。
>>> backward_3p_ma_shifted = x.rolling(window=3).mean().shift(-1) >>> pd.concat([x, backward_3p_ma_shifted], axis=1) 0 1 0 1 NaN 1 2 2.0 2 3 3.0 3 4 4.0 4 5 5.0 5 6 6.0 6 7 7.0 7 8 8.0 8 9 9.0 9 10 10.0 10 11 11.0 11 12 NaN
そのため、平均をとる要素数が偶数のときに困ったことが起こる。
平均をとる要素数が偶数のときの問題点について
試しに、平均をとる要素数を 4 点に増やして、そのまま計算してみよう。
>>> centerd_4p_ma = x.rolling(window=4, center=True).mean() >>> centerd_4p_ma 0 NaN 1 NaN 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10 10.5 11 NaN dtype: float64
すると、計算結果に端数が出ている。
原系列と比較すると、対応関係に 0.5 の遅れがあることがわかる。
>>> pd.concat([x, centerd_4p_ma], axis=1) 0 1 0 1 NaN 1 2 NaN 2 3 2.5 3 4 3.5 4 5 4.5 5 6 5.5 6 7 6.5 7 8 7.5 8 9 8.5 9 10 9.5 10 11 10.5 11 12 NaN
つまり、中心化移動平均では平均をとる要素数が偶数と奇数のときで計算方法を変えなければいけない。
要素数が偶数のときの計算方法
要素数が偶数のときの中心化移動平均は、計算が 2 段階に分かれている。 はじめに、後方移動平均をそのまま計算する。
>>> backward_4p_ma =x.rolling(window=4).mean() >>> backward_4p_ma 0 NaN 1 NaN 2 NaN 3 2.5 4 3.5 5 4.5 6 5.5 7 6.5 8 7.5 9 8.5 10 9.5 11 10.5 dtype: float64
その上で、移動平均に使った要素数の半分だけデータをずらし、もう一度要素数 2 で平均を取り直す。
centerd_4p_ma = backward_4p_ma.shift(-2).rolling(window=2).mean()
原系列との対応関係を確認すると、遅れが解消していることがわかる。
>>> pd.concat([x, centerd_4p_ma], axis=1) 0 1 0 1 NaN 1 2 NaN 2 3 3.0 3 4 4.0 4 5 5.0 5 6 6.0 6 7 7.0 7 8 8.0 8 9 9.0 9 10 10.0 10 11 NaN 11 12 NaN
別のデータで中心化移動平均を計算してみる
もうちょっとちゃんとしたデータでも計算してみよう。 次のサンプルコードでは、旅客機の乗客数の推移に対して 12 点で中心化移動平均を計算している。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- from calendar import month_name import seaborn as sns from matplotlib import pyplot as plt import pandas as pd from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() def main(): # 航空機の乗客を記録したデータセットを読み込む df = sns.load_dataset('flights') # 月の名前を数字に直す month_name_mappings = {name: str(n).zfill(2) for n, name in enumerate(month_name)} df['month'] = df['month'].apply(lambda x: month_name_mappings[x]) # 年と月を結合したカラムを用意する df['year-month'] = df.year.astype(str) + '-' + df.month.astype(str) df['year-month'] = pd.to_datetime(df['year-month'], format='%Y-%m') # 原系列 sns.lineplot(data=df, x='year-month', y='passengers', label='original') # 中心化移動平均 df['passengers-cma'] = df['passengers'].rolling(window=12).mean().shift(-6).rolling(2).mean() sns.lineplot(data=df, x='year-month', y='passengers-cma', label='CMA') # グラフを表示する plt.show() if __name__ == '__main__': main()
上記を実行してみる。
$ python flightscma.py
得られるグラフが次のとおり。
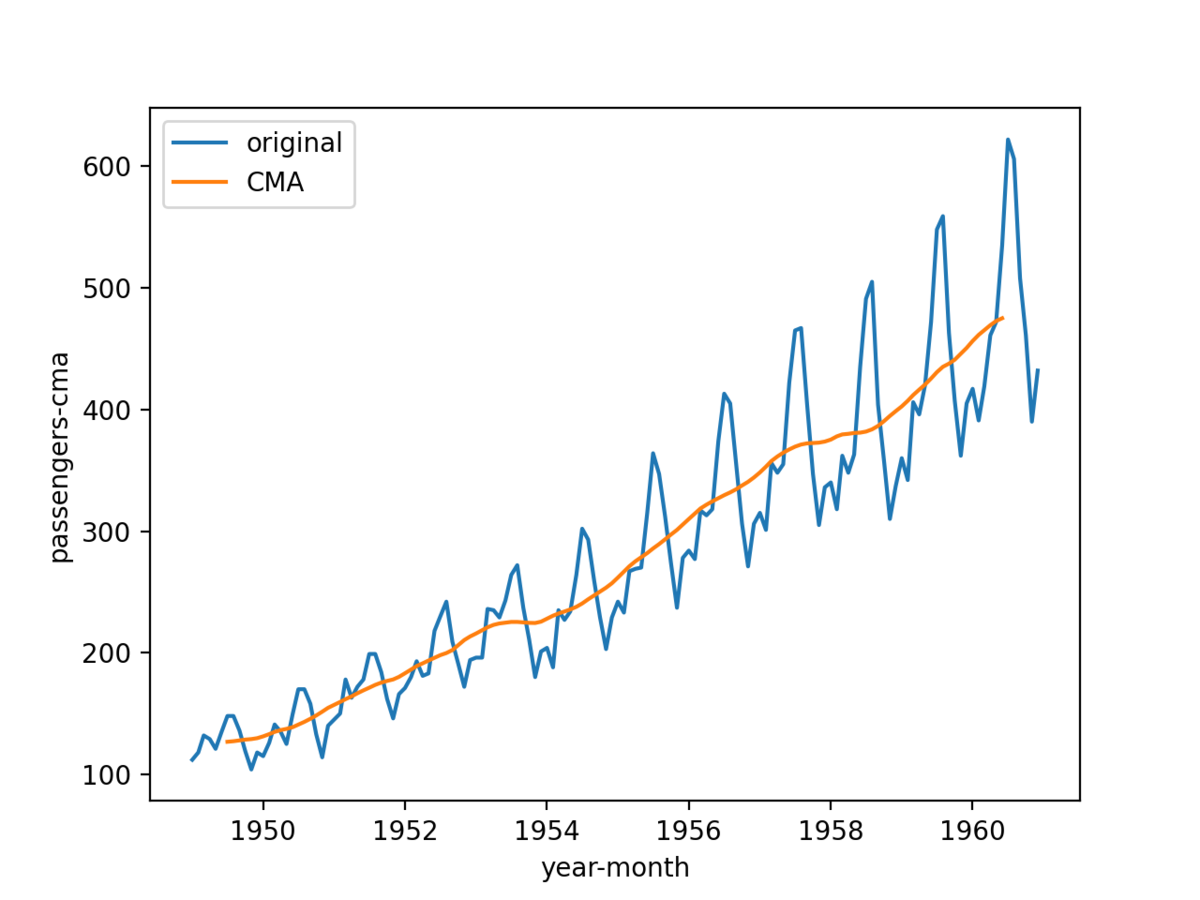
ここまでデータ点数が多いと、正直 0.5 の遅れとか言われてもよくわからないけど、これで計算できているはず。

時系列解析: 自己回帰型モデル・状態空間モデル・異常検知 (Advanced Python)
- 作者:直希, 島田
- 発売日: 2019/09/07
- メディア: 単行本

- 作者:もみじあめ
- 発売日: 2020/02/29
- メディア: Kindle版