機械学習を用いるタスクで、モデルの解釈可能性 (Interpretability) が重要となる場面がある。 今回は、モデルの解釈可能性を得る手法のひとつとして PDP (Partial Dependence Plot: 部分従属プロット) を扱ってみる。 PDP を使うと、モデルにおいて説明変数と目的変数がどのような関係にあるか理解する上で助けになることがある。 なお、今回は PDP を計算・描画するのに専用のライブラリは使わず、自分で実装してみることにした。
使った環境は次のとおり。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.14.6 BuildVersion: 18G4032 $ python -V Python 3.7.7
下準備
まずは、あらかじめ必要なパッケージをインストールしておく。
$ pip install scikit-learn pandas matplotlib
題材とするデータセットとモデルについて
今回は scikit-learn 付属の糖尿病 (Diabetes) データセットを題材として話を進める。 このデータセットは、患者の情報が説明変数で、糖尿病の進行具合が目的変数となっている。
たとえば、これをランダムフォレストで学習させることを考えてみよう。 次のサンプルコードでは、モデルにデータセットを学習させた上で、特徴量の重要度をグラフにプロットしている。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np from matplotlib import pyplot as plt from sklearn import datasets from sklearn.ensemble import RandomForestRegressor def main(): # 糖尿病データセットを読み込む dataset = datasets.load_diabetes() X, y = dataset.data, dataset.target # ランダムフォレストを学習させる clf = RandomForestRegressor(n_estimators=100, random_state=42) clf.fit(X, y) # ジニ不純度を元に計算した重要度を得る importances = clf.feature_importances_ feature_names = np.array(dataset.feature_names) sorted_indices = np.argsort(importances)[::-1] # 重要度をプロットする plt.bar(feature_names[sorted_indices], importances[sorted_indices]) plt.show() if __name__ == '__main__': main()
上記をファイルに保存して実行してみよう。
$ python giniimp.py
すると、次のような棒グラフが得られる。
モデルにおいて、s5 や bmi といった特徴量が重要視されていることがわかる。

なお、ここで計算している重要度は決定木系のモデルに特有のもの。 具体的には、決定木がデータを分割する上でジニ不純度をうまく下げることのできた特徴量を重要なものと判断している。 一般的には Gini Importance や Split Importance と呼ばれている。
この他にも、モデルに依存しない特徴量の重要度として Permutation Importance などが知られている。
BMI に着目してみる
先ほど計算した重要度では、モデルが特定の特徴量を予測する上で重要視していることがわかった。 しかし、その特徴量が予測する上でどのように重要とされているのかはわからない。
ここでは、先ほど重要とされた BMI にひとまず着目してみよう。 まずは、BMI に含まれる値を確認しておく。 次のサンプルコードでは、BMI に含まれる値をヒストグラムにプロットしている。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import pandas as pd from sklearn import datasets from matplotlib import pyplot as plt def main(): dataset = datasets.load_diabetes() X, y = dataset.data, dataset.target # 特定カラムのヒストグラムを描く df = pd.DataFrame(X, columns=dataset.feature_names) df['bmi'].plot.hist() plt.show() if __name__ == '__main__': main()
上記を実行してみよう。
$ python bmihist.py
すると、次のようなグラフが得られる。
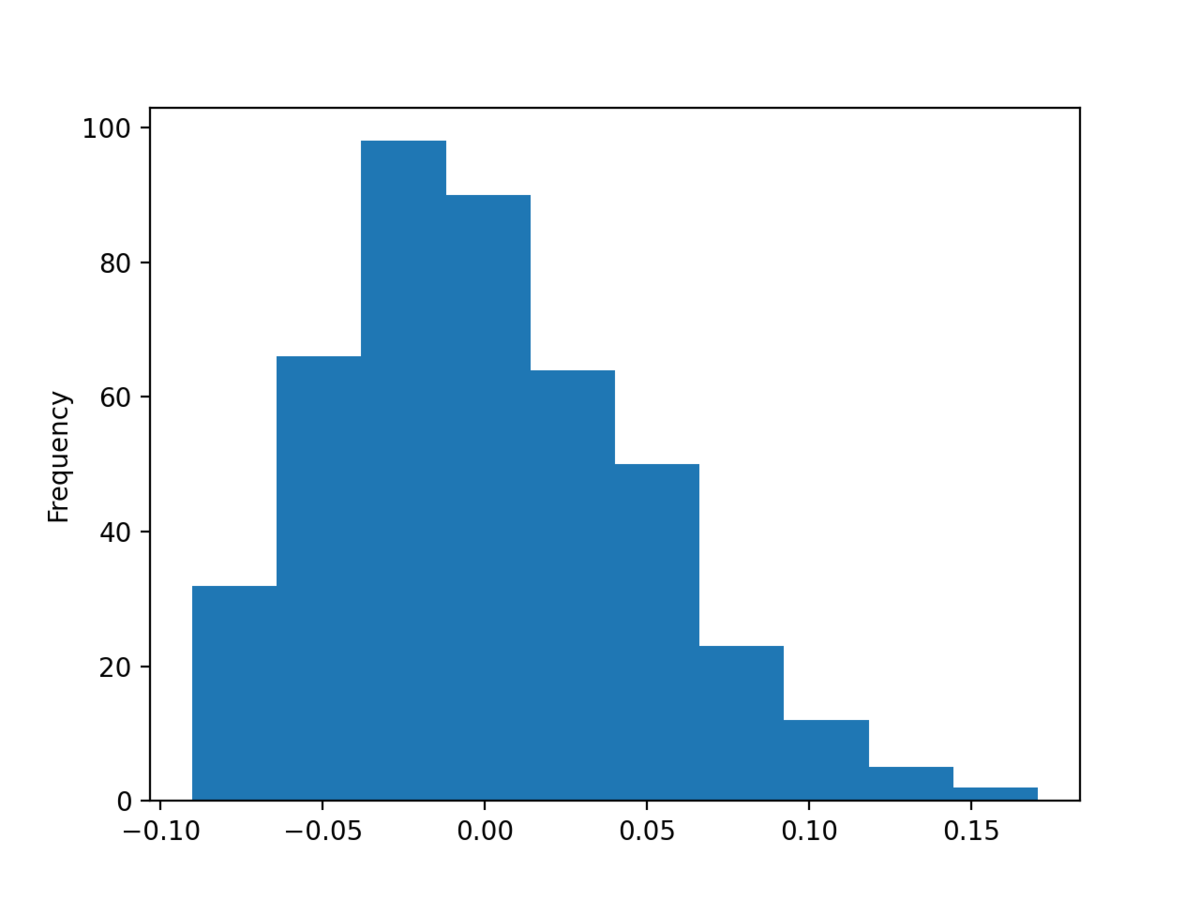
上記のグラフから、BMI は -0.1 ~ +0.15 前後の範囲に値を持つことがわかった。
特定の行 (患者) について BMI を変化させて予測を観察する
続いて、今回扱う PDP の根底となる考え方を説明する。 それは、ある行 (患者) において他の条件は固定したまま特定の説明変数を変化させたとき、予測がどのように変化するかを観察するというもの。
今回であれば、その他の特徴量は固定したまま、BMI の値を色々と変化させたとき、予測がどう変化するかを観察する。 次のサンプルコードでは、先頭の 1 行 (1 人の患者) について BMI を 10 段階で変化させながらモデルの予測を折れ線グラフにプロットしている。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np import pandas as pd from sklearn import datasets from sklearn.ensemble import RandomForestRegressor from matplotlib import pyplot as plt def main(): # データセットを読み込む dataset = datasets.load_diabetes() X, y = dataset.data, dataset.target df = pd.DataFrame(X, columns=dataset.feature_names) # あらかじめ解釈したいモデルを学習させておく clf = RandomForestRegressor(n_estimators=100, random_state=42) clf.fit(X, y) # 特定のカラムが取りうる値を等間隔で計算する resolution = 10 # 間隔数 target_column = 'bmi' # 対象とするカラム名 min_, max_ = df[target_column].quantile([0, 1]) candidate_values = np.linspace(min_, max_, resolution) # 例として先頭の行を取り出す target_row = df.iloc[0] # 特定のカラムの値を入れかえながらモデルに予測させる y_preds = np.zeros(resolution) for trial, candidate_value in enumerate(candidate_values): target_row[target_column] = candidate_value y_preds[trial] = clf.predict([target_row]) # 予測させた結果をプロットする plt.plot(candidate_values, y_preds) plt.xlabel('factor') plt.ylabel('target') plt.show() if __name__ == '__main__': main()
上記を実行してみよう。
$ python icehead.py
すると、次のようなグラフが得られる。 どうやら BMI の値が大きくなると、概ね病気の進行具合も進んでいると判断されるようだ。
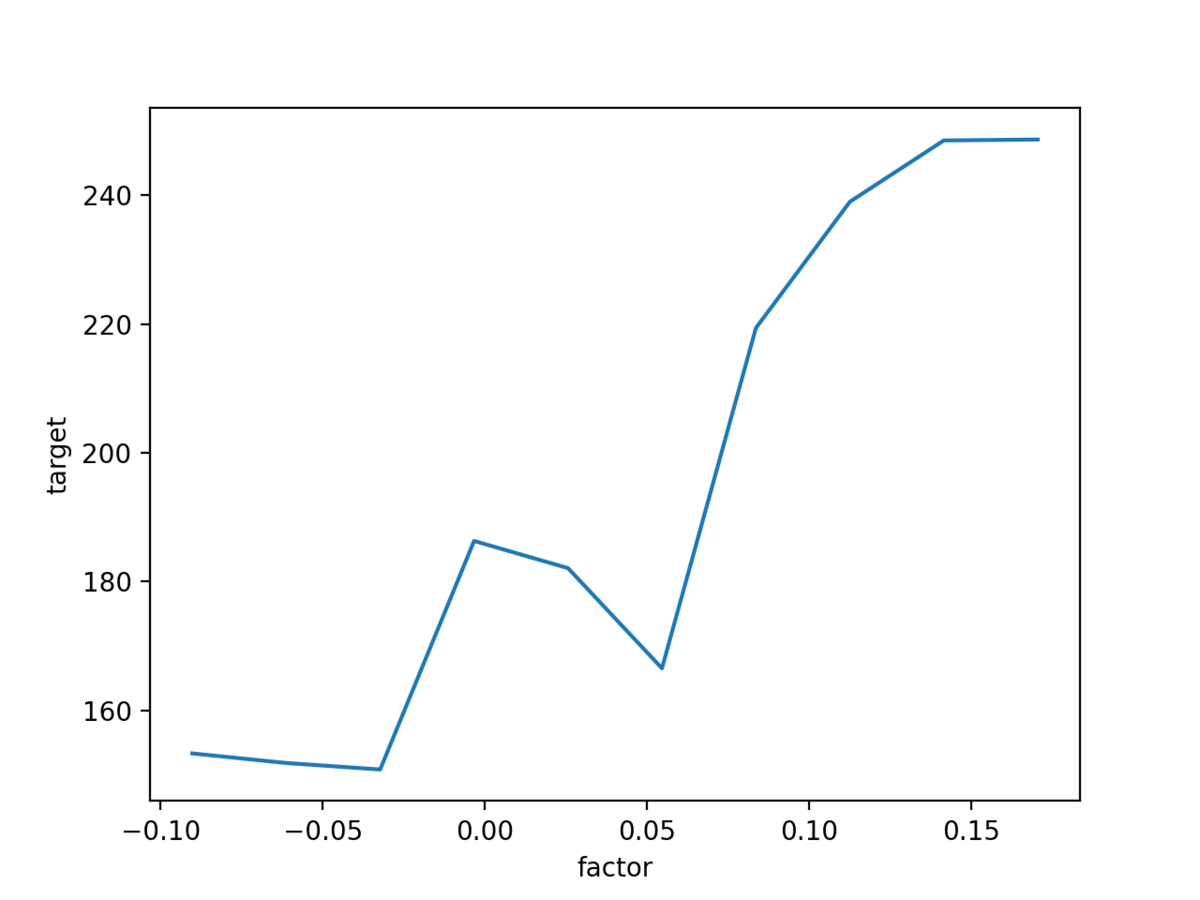
とはいえ、一人の患者だけを見て判断するのは早計なはず。 もっと、たくさんの行も確認して、より大局的な傾向を把握したい。
次のサンプルコードでは、全データの 10% をサンプリングした上で先ほどと同じことをしている。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np import pandas as pd from sklearn import datasets from matplotlib import pyplot as plt from sklearn.ensemble import RandomForestRegressor def main(): dataset = datasets.load_diabetes() X, y = dataset.data, dataset.target df = pd.DataFrame(X, columns=dataset.feature_names) clf = RandomForestRegressor(n_estimators=100, random_state=42) clf.fit(X, y) resolution = 10 target_column = 'bmi' min_, max_ = df[target_column].quantile([0, 1]) candidate_values = np.linspace(min_, max_, resolution) # いくつかの行について、特定のカラムの値を入れかえながらモデルに予測させる sampling_factor = 0.1 sampled_df = df.sample(frac=sampling_factor, random_state=42) y_preds = np.zeros((len(sampled_df), resolution)) for index, (_, target_row) in enumerate(sampled_df.iterrows()): for trial, candidate_value in enumerate(candidate_values): target_row[target_column] = candidate_value y_preds[index][trial] = clf.predict([target_row]) # 予測させた結果をプロットする for y_pred_row in y_preds: plt.plot(candidate_values, y_pred_row, color='b') plt.xlabel('factor') plt.ylabel('target') plt.show() if __name__ == '__main__': main()
上記を実行してみよう。
$ python ice.py
すると、次のようなグラフが得られる。 やはり、概ね BMI が大きくなると病気の進行具合も進んでいると判断できるようだ。
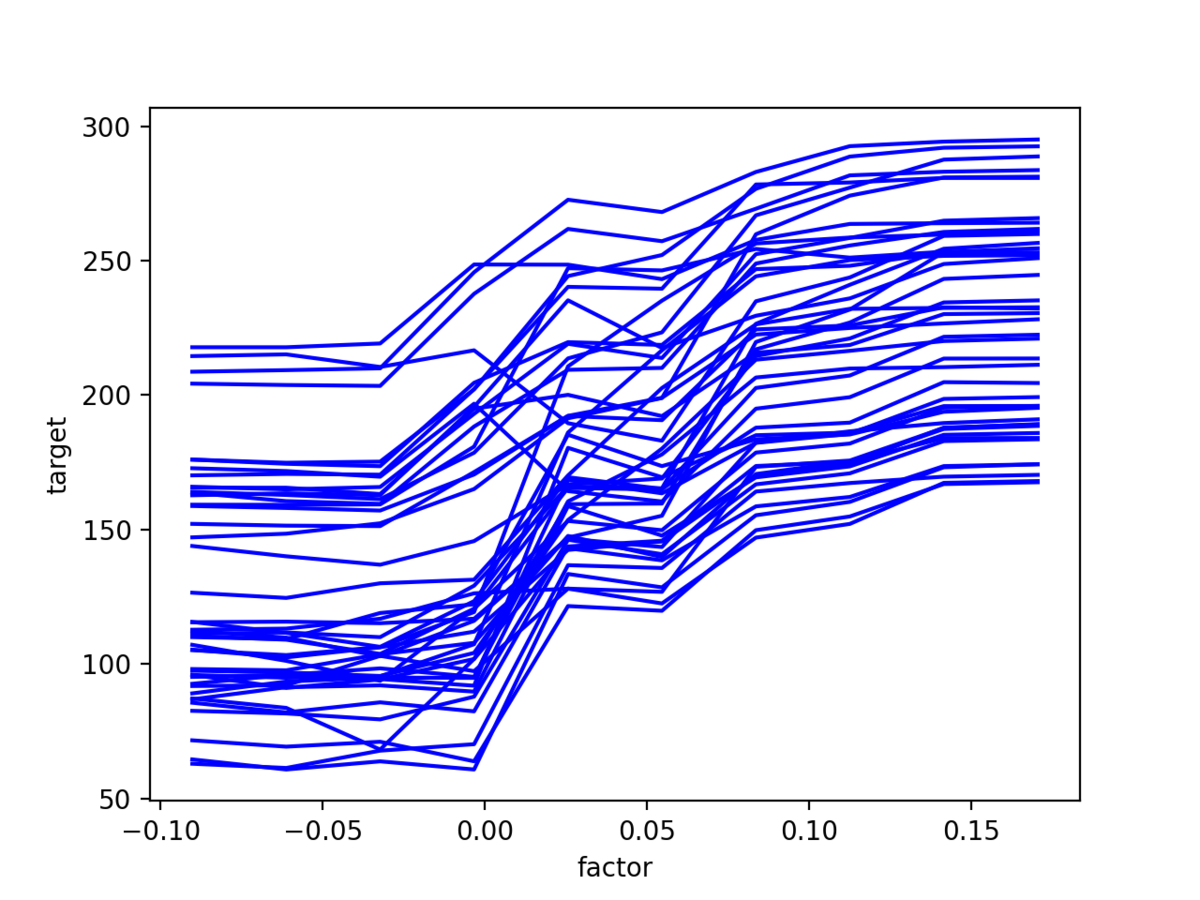
上記の手法を ICE (Individual Conditional Expectation: 個別条件付き期待値) Plot という。
ICE の要約統計量をグラフにプロットする
ICE Plot を使うことで、個別の行について説明変数と目的変数の関係性を把握できる。 一方で、たくさん折れ線グラフがあるとぶっちゃけ見にくい。 そこで、平均値などの要約統計量をグラフにプロットしてみよう。
次のサンプルコードでは ICE の平均値と、バラつきを確認するために 1 SD (Standard Division: 標準偏差) を描画している。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np import pandas as pd from matplotlib import pyplot as plt from sklearn import datasets from sklearn.ensemble import RandomForestRegressor def main(): dataset = datasets.load_diabetes() X, y = dataset.data, dataset.target df = pd.DataFrame(X, columns=dataset.feature_names) clf = RandomForestRegressor(n_estimators=100, random_state=42) clf.fit(X, y) resolution = 10 target_column = 'bmi' min_, max_ = df[target_column].quantile([0, 1]) candidate_values = np.linspace(min_, max_, resolution) # いくつかの行について、特定のカラムの値を入れかえながらモデルに予測させる sampling_factor = 0.5 sampled_df = df.sample(frac=sampling_factor) y_preds = np.zeros((len(sampled_df), resolution)) for index, (_, target_row) in enumerate(sampled_df.iterrows()): for trial, candidate_value in enumerate(candidate_values): target_row[target_column] = candidate_value y_preds[index][trial] = clf.predict([target_row]) # 予測させた結果をプロットする mean_y_preds = y_preds.mean(axis=0) # 平均 sd_y_preds = y_preds.std(axis=0) # 標準偏差 # 平均 ± 1 SD を折れ線グラフにする plt.plot(candidate_values, mean_y_preds) plt.fill_between(candidate_values, mean_y_preds - sd_y_preds, mean_y_preds + sd_y_preds, alpha=0.5) plt.xlabel('factor') plt.ylabel('target') plt.show() if __name__ == '__main__': main()
上記を実行してみよう。
$ python pdp.py
すると、次のようなグラフが得られる。 ICE をたくさんプロットするよりも見やすい。 そして、このグラフこそ、今回の本題である PDP というらしい。
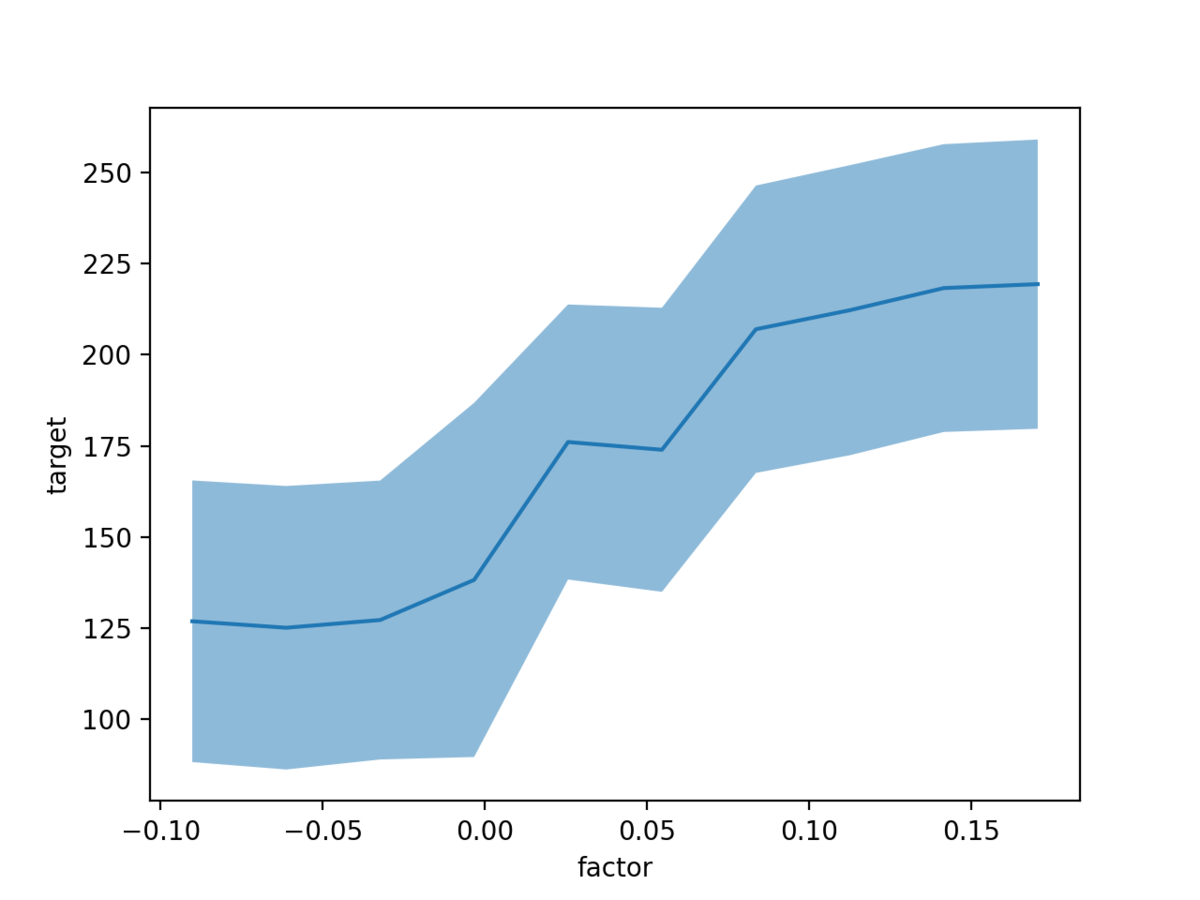
同じ要領で、他の特徴量についても PDP をプロットしていくことで説明変数と目的変数の関係性を把握する。
補足
なお、scikit-learn には PDP を描画するための専用の API もある。 今回は勉強がてら自分で書いてみたけど、普段はこちらを使う方が手っ取り早いはず。
いじょう。

- 作者:もみじあめ
- 発売日: 2020/02/29
- メディア: Kindle版
