以前、このブログで相関係数について解説した記事を書いたことがある。 相関係数というのは、データセットのある次元とある次元の関連性を示すものだった。
この相関係数を、データセットの各次元ごとに計算したものを相関行列と呼ぶ。 データ分析の世界では、それぞれの次元の関連性を見るときに、この相関行列を計算することがある。 また、それを見やすくするためにヒートマップというグラフを用いて図示することが多い。
今回は Python を使って相関行列を計算すると共にヒートマップを描いてみることにした。
使った環境は次の通り。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.12.4 BuildVersion: 16E195 $ python --version Python 3.5.3
下準備
今回は、相関行列の計算には NumPy を、グラフの描画には seaborn を使うのでインストールしておく。
最後の scikit-learn については、相関行列の計算に使うデータセットを読み込むためだけに使っている。
$ pip install seaborn numpy scikit-learn
相関行列を計算してみる
まずはヒートマップの描く以前に相関行列の計算から。 データセットにはみんな大好きアイリス (あやめ) データセットを用いる。 これは 150 行 4 次元の構造になっている。
>>> from sklearn import datasets >>> dataset = datasets.load_iris() >>> features = dataset.data >>> features.shape (150, 4)
相関行列の計算には NumPy の corrcoef() 関数が使える。
この関数には、相関行列を計算したい次元をリストの形で渡す。
すごくベタに書くとしたら、こんな感じ。
>>> import numpy as np >>> np.corrcoef([features[:, 0], features[:, 1], features[:, 2], features[:, 3]]) array([[ 1. , -0.10936925, 0.87175416, 0.81795363], [-0.10936925, 1. , -0.4205161 , -0.35654409], [ 0.87175416, -0.4205161 , 1. , 0.9627571 ], [ 0.81795363, -0.35654409, 0.9627571 , 1. ]])
上記には、それぞれの次元ごとの相関係数が格納されている。 対角要素が全て 1 になっているのは、全く同じデータ同士の相関係数は 1 になるため。
ただ、実際には上記のようなベタ書きをする必要はない。 次元ごとにリストで、というのはようするに行と列を入れ替えれば良いということ。 つまり M 行 N 列のデータなら N 行 M 列に直して渡すことになる。
これは NumPy 行列なら transpose() メソッドで実現できる。
>>> features.transpose().shape (4, 150)
ようするに、こうなる。
>>> np.corrcoef(features.transpose()) array([[ 1. , -0.10936925, 0.87175416, 0.81795363], [-0.10936925, 1. , -0.4205161 , -0.35654409], [ 0.87175416, -0.4205161 , 1. , 0.9627571 ], [ 0.81795363, -0.35654409, 0.9627571 , 1. ]])
相関行列はこれで計算できた。
ヒートマップを描いてみる
続いては、先ほどの相関行列をヒートマップにしてみよう。
Python のグラフ描画ライブラリの seaborn には、あらかじめヒートマップを描くための API が用意されている。
次のサンプルコードではアイリスデータセットの相関行列をヒートマップで図示している。 それぞれの行の説明についてはコメントで補足している。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from matplotlib import pyplot as plt import seaborn as sns from sklearn import datasets def main(): # アイリスデータセットを読み込む dataset = datasets.load_iris() features = dataset.data feature_names = dataset.feature_names # N 行 M 列を M 行 N 列に変換して相関行列を計算する correlation_matrix = np.corrcoef(features.transpose()) # 相関行列のヒートマップを描く sns.heatmap(correlation_matrix, annot=True, xticklabels=feature_names, yticklabels=feature_names) # グラフを表示する plt.show() if __name__ == '__main__': main()
上記を実行すると、次のようなグラフが得られる。
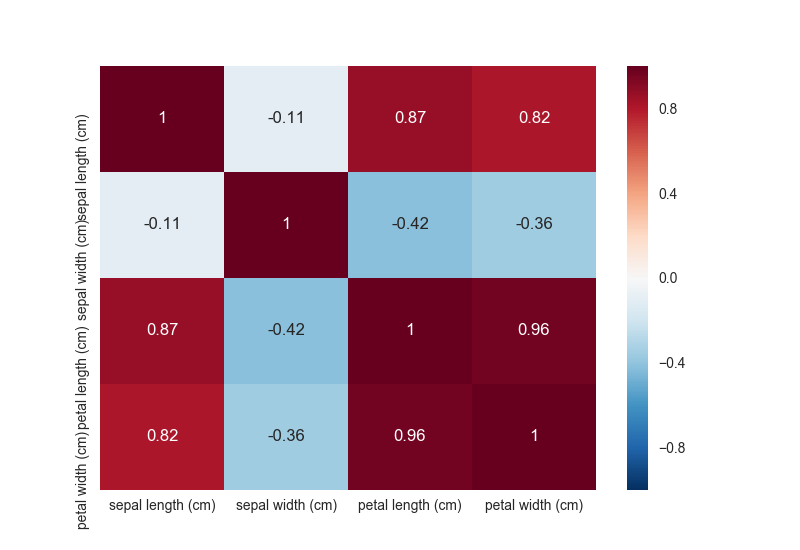
このヒートマップでは、正の相関が強いものほど赤く、負の相関が強いものほど青く図示されている。 相関がないものについては色が薄いことから白に近づくことになる。 上記を見ると、アイリスデータセットには相関の強い次元が多いことが分かる。
主成分分析した結果の相関行列でヒートマップを描いてみる
ここで一つ気になったことを試してみることにした。 主成分分析した結果を相関行列にしてヒートマップで描いてみる、というものだ。 主成分分析とは何ぞや、ということは以下のブログエントリで書いた。
理屈の上では、主成分分析した結果は互いに直交した次元になるため相関しないはず。 これを相関行列とヒートマップで確かめてみよう、ということ。
次のサンプルコードでは、アイリスデータセットを主成分分析している。 そして、分析した内容に対して相関行列を計算してヒートマップを描いた。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from matplotlib import pyplot as plt import seaborn as sns from sklearn import datasets from sklearn.decomposition import PCA def main(): # アイリスデータセットを読み込む dataset = datasets.load_iris() features = dataset.data # 特徴量を主成分分析する pca = PCA() pca.fit(features) # 分析にもとづいて特徴量を主成分に変換する transformed_features = pca.fit_transform(features) # 主成分の相関行列を計算する correlation_matrix = np.corrcoef(transformed_features.transpose()) # 主成分の相関行列をヒートマップで描く feature_names = ['PCA{0}'.format(i) for i in range(features.shape[1])] sns.heatmap(correlation_matrix, annot=True, xticklabels=feature_names, yticklabels=feature_names) # グラフを表示する plt.show() if __name__ == '__main__': main()
上記を実行すると、次のようなグラフが得られる。
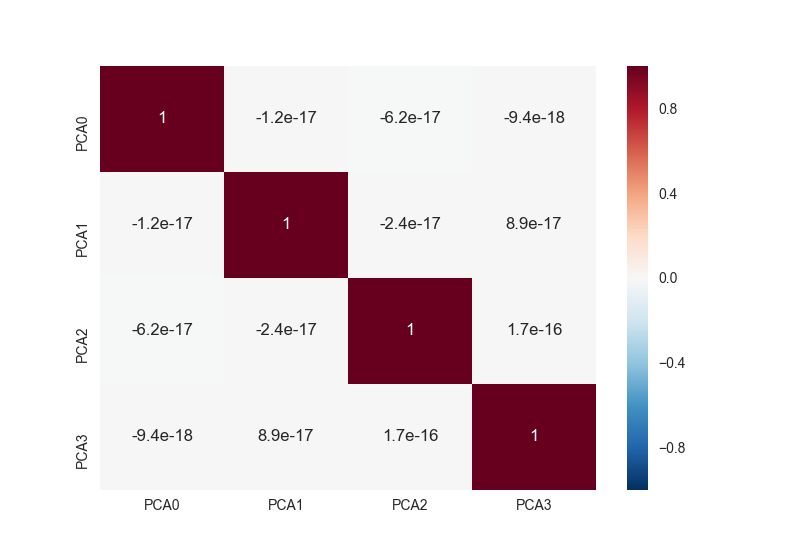
見事に真っ白で、互いに相関が全然ないことが分かる。 理屈通りの結果になった。
まとめ
- 二つの次元の関連性を調べるには相関係数を用いる
- データセットに含まれる全ての次元で相関係数を計算したものを相関行列と呼ぶ
- 相関行列はヒートマップというグラフで図示することが多い
- 主成分分析した結果の相関行列は対角要素を覗いてゼロになる
めでたしめでたし。

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログ (1件) を見る