データエンジニアリングの分野では、分類精度などを高めるためにデータの前処理が重要となってくる。 今回は、そんな前処理の中でも無名数化と呼ばれる手法について見ていく。
無名数化というのは、具体的にはデータに含まれる次元の単位をなくす処理のことを指している。 単位というのは、例えば長さなら cm 重さなら kg といったもの。 単位のついた数値のことを名数、単位のない数値のことを無名数と呼ぶ。 単位の情報がある状態から、ない状態に変換することから無名数化と呼ばれる。
無名数化のメリットは使う手法によって異なるものの、基本的には次元による数値の大小の影響がなくなるところ。 使うモデルによっては数値の大きさに影響を受けやすいものがある。 例えば最近傍法などはその代表で、数値の大きな次元に影響を受けやすい。
使った環境は次の通り。 扱うデータセットにはアイリス (あやめ) データセットを用いた。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.12.6 BuildVersion: 16G29 $ python --version Python 3.6.3
下準備として、今回のサンプルコードで使うライブラリをインストールしておこう。
$ pip install scikit-learn matplotlib scipy
標準化
まず最初に紹介するのは標準化と呼ばれる手法から。 この手法は統計の世界でもよく使われるものになっている。 一般正規分布を標準化することで標準正規分布が得られることが有名。
これは、具体的にはデータの各要素からデータの平均値を引いて標準偏差で割る手法をいう。 数式で表すと、次のようになる。 標準化した値のことを Z スコアと呼んだりすることもある。
ここで はデータの集合、
はその平均値、
は標準偏差を表している。
が標準化した後のデータ、Z スコアということ。
データを標準化して Z スコアにすると、その平均値は 0 で標準偏差は 1 になる。
実際にアイリスデータセットを使って標準化するとどうなるのか試してみよう。 次のサンプルコードではアイリスデータセットの花びらの長さと幅の二次元を取り出して標準化している。 そして変換前と変換後でどのように分布が変わるのかを図示している。
#!/usr/bin/env python # -*- coding: utf-8 -*- from sklearn import datasets from matplotlib import pyplot as plt def main(): # アイリスデータセットをロードする iris = datasets.load_iris() # petal length (花びらの長さ), petal width (花びらの幅) だけ取り出す X = iris.data[:, 2:] # 標準化する (平均を引いて標準偏差で割る) Z = (X - X.mean(axis=0)) / X.std(axis=0) # 標準化した後の母数を表示する Z_mean = Z.mean(axis=0) print('標準化後の平均値: {mean}'.format(mean=Z_mean)) Z_std = Z.std(axis=0) print('標準化後の標準偏差: {std}'.format(std=Z_std)) plt.scatter(X[:, 0], X[:, 1], label='before') # 標準化前 plt.scatter(Z[:, 0], Z[:, 1], label='after') # 標準化後 plt.ylim((-2, 3)) plt.xlim((-2, 8)) plt.xlabel('petal length') plt.ylabel('petal width') plt.plot([0, 0], [-2, 3], 'k--') plt.plot([-2, 8], [0, 0], 'k--') plt.grid(True) plt.legend() plt.show() if __name__ == '__main__': main()
上記をファイルに保存して実行してみよう。 プログラムの中では標準化後の次元の平均値と標準偏差を出力している。
$ python standarding.py 標準化後の平均値: [ -1.48251781e-15 -1.62314606e-15] 標準化後の標準偏差: [ 1. 1.]
平均値はとても小さくなってほとんど 0 になっているし、標準偏差はちゃんと 1 になっている。
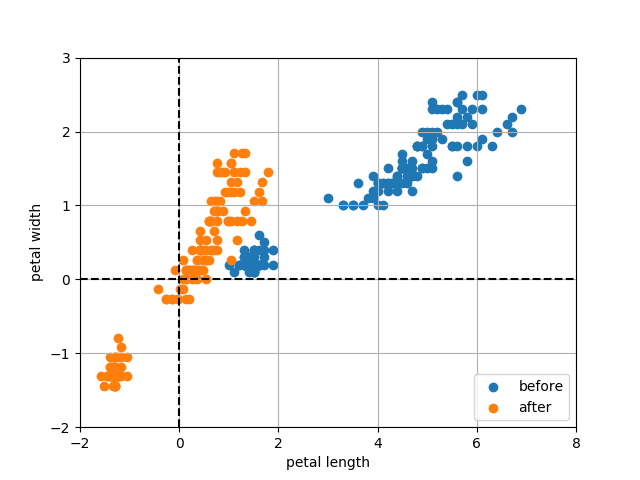
標準化前と標準化後の散布図は次の通り。 標準化後は分布の中心が原点になって、バラつきも小さくなっていることが分かる。
無相関化
続いては無相関化を扱う。 無相関化とは、文字通りだけど次元間の相関をなくす処理のことをいう。
データに複数の次元があるとき、それぞれの次元の間に相関があるか否かはデータエンジニアリングにおいて重要なポイントとなる。 なぜなら、二つの次元に相関があるとき、それはほとんど同じものが二つあることを意味しているため。 ある次元 A と B の間に正の強い相関があるとすれば、次元 A の値が大きいときは次元 B の値を大きいことになる。 だとすれば、分類や回帰をするときには A か B どちらか一方の次元さえあれば事足りてしまうことを意味する。
取り扱う次元の数が増えることは、時間・空間計算量が指数的に増加することを意味している。 つまり、データセットの各次元にはなるべく相関が少ない方が好ましい。 とはいえ、元から相関のないデータばかりではないことから、無相関化という処理で相関を取り除くというわけだ。 無相関化すれば、各次元間の相関は 0 になる。
無相関化の具体的なやり方としては、分散共分散行列の固有値問題を解くのが最初の一歩となる。 分散共分散行列というのは対角成分が分散、それ以外が各次元間の共分散になった行列のこと。 ひとまず、その分散共分散行列の固有値問題を解いて得られる固有ベクトルが重要になる。 この固有ベクトルのことを回転行列と呼んで、この回転行列を使ってデータを線形変換する。 数式に表すと次の通り。
上記において が分散共分散行列の固有値問題を解いて得られた回転行列とする。
線形変換するデータが
で、した結果が
となる。
理論的な部分を細かく説明しても分かりにくくなるので、とりあえずこれくらいに抑えておく。
実際にデータを無相関化するサンプルコードを次に示す。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from sklearn import datasets from matplotlib import pyplot as plt def main(): iris = datasets.load_iris() X = iris.data[:, 2:] # 分散共分散行列を計算する Sigma = np.cov(X, rowvar=0) # 固有値、固有ベクトル (回転行列) を得る _, S = np.linalg.eig(Sigma) # 回転行列を使ってデータを線形変換する y = np.dot(S.T, X.T).T # 無相関化後の分散共分散行列を計算する y_cov = np.cov(y, rowvar=0) print('無相関化後の分散共分散行列: {cov}'.format(cov=y_cov)) plt.scatter(X[:, 0], X[:, 1], label='before') plt.scatter(y[:, 0], y[:, 1], label='after') plt.ylim((-2, 3)) plt.xlim((-2, 8)) plt.xlabel('petal length') plt.ylabel('petal width') plt.plot([0, 0], [-2, 3], 'k--') plt.plot([-2, 8], [0, 0], 'k--') plt.grid(True) plt.legend() plt.show() if __name__ == '__main__': main()
上記をファイルに保存して実行してみよう。 すると、無相関化した後の各次元の分散共分散行列が得られる。 確認すると、二つの次元の共分散はとても小さい値になっていることから相関が取り除かれたことが分かる。
$ python decorrelating.py 無相関化後の分散共分散行列: [[ 3.65937449e+00 -1.43062296e-16] [ -1.43062296e-16 3.62192472e-02]]
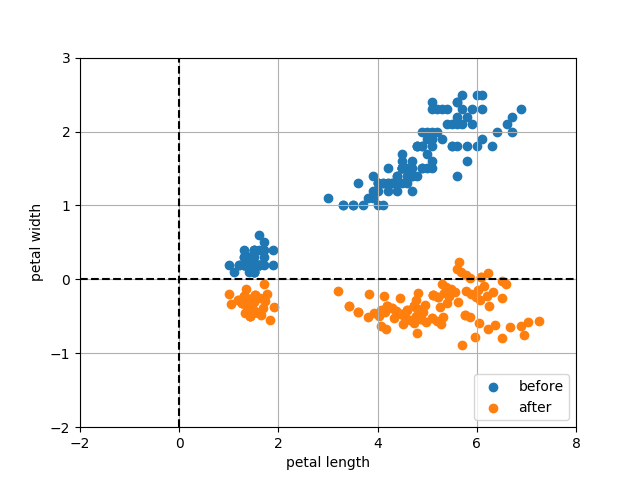
得られる散布図は次の通り。 分布が右上がりや右下がりだと相関があることを意味している。 元々の分布は右上がりなので正の相関があったことを読み取れる。 それに対し無相関化後の分布は横にまっすぐ分布していることから相関があることは読み取れない。
無相関化と主成分分析
実は無相関化と主成分分析 (PCA) には深い関わりがある。 というより、やっていることはほとんど同じといっていい。 具体的には無相関化に中心化という処理を加えたものが主成分分析になる。 中心化というのは、標準化でやっていた「平均を引く」処理のこと。 これをするとデータの分布の中心が原点になるので、文字通り中心化となる。
次のサンプルコードは先ほどとほとんど変わらない。 変更点は、無相関化するデータをあらかじめ中心化しているのみ。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from sklearn import datasets from matplotlib import pyplot as plt def main(): iris = datasets.load_iris() X = iris.data[:, 2:] # データを中心化する (平均を引くことで平均を 0 にする) X_centerized = X - X.mean(axis=0) # 分散共分散行列を計算する Sigma = np.cov(X, rowvar=0) # 固有値、固有ベクトル (回転行列) を得る _, S = np.linalg.eig(Sigma) # 回転行列を使ってデータを線形変換する y = np.dot(S.T, X_centerized.T).T # 無相関化後の分散共分散行列を計算する y_cov = np.cov(y, rowvar=0) print('無相関化後の分散共分散行列: {cov}'.format(cov=y_cov)) plt.scatter(X[:, 0], X[:, 1], label='before') plt.scatter(y[:, 0], y[:, 1], label='after') plt.ylim((-2, 3)) plt.xlim((-4, 8)) plt.xlabel('petal length') plt.ylabel('petal width') plt.plot([0, 0], [-2, 3], 'k--') plt.plot([-2, 8], [0, 0], 'k--') plt.grid(True) plt.legend() plt.show() if __name__ == '__main__': main()
ファイルに保存して実行してみよう。
$ python centerizing.py 無相関化後の分散共分散行列: [[ 3.65937449e+00 -1.28159973e-16] [ -1.28159973e-16 3.62192472e-02]]
すると、次のような散布図が得られる。 先ほどの無相関化した散布図を中心に移動させた感じ。
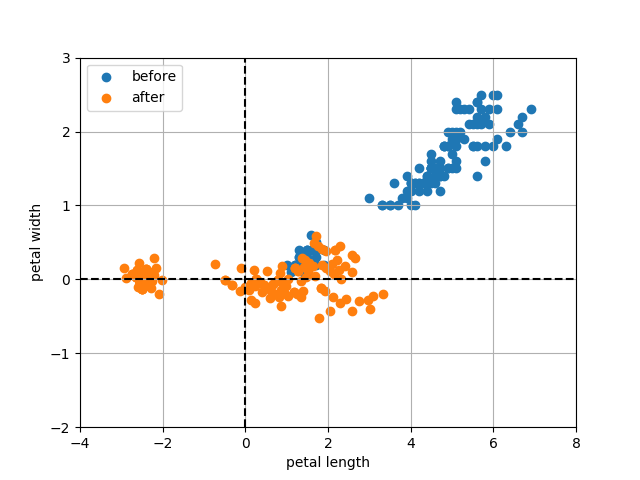
上記の散布図の形をちょっと覚えておいてほしい。
続いて登場するサンプルコードは scikit-learn を使って同じデータを主成分分析している。
scikit-learn では sklearn.decomposition.PCA を使って主成分分析ができる。
以下では、主成分分析した結果から第一主成分と第二主成分を散布図にプロットしている。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from sklearn import datasets from sklearn.decomposition import PCA from matplotlib import pyplot as plt def main(): iris = datasets.load_iris() X = iris.data[:, 2:] # 主成分分析 pca = PCA() pca.fit(X) y = pca.fit_transform(X) # 第一・第二主成分の分散共分散行列を計算する y_cov = np.cov(y, rowvar=0) print('無相関化後の分散共分散行列: {cov}'.format(cov=y_cov)) plt.scatter(X[:, 0], X[:, 1], label='before') plt.scatter(y[:, 0], y[:, 1], label='after') plt.ylim((-2, 3)) plt.xlim((-4, 8)) plt.xlabel('petal length') plt.ylabel('petal width') plt.plot([0, 0], [-2, 3], 'k--') plt.plot([-2, 8], [0, 0], 'k--') plt.grid(True) plt.legend() plt.show() if __name__ == '__main__': main()
上記を保存して実行してみよう。
$ python pca.py 無相関化後の分散共分散行列: [[ 3.65937449e+00 1.26669741e-17] [ 1.26669741e-17 3.62192472e-02]]
次のような散布図が得られるので、さきほどの散布図と比較してほしい。 全く同じものになっているはずだ。
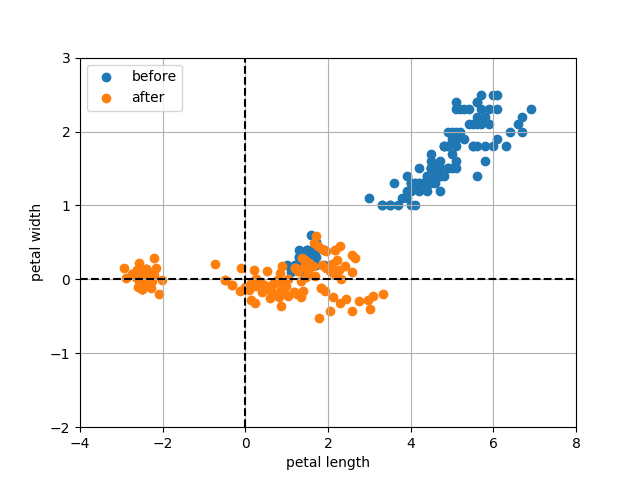
つまり、主成分分析というのは中心化したデータを無相関化することと同義ということになる。
白色化
続いては白色化という処理を紹介する。 これは、無相関化した結果を標準化したような考えに近い。 つまり、白色化するとデータは各次元間の相関がなくなった上に平均が 0 で標準偏差が 1 になる。
ただし、やり方は少し複雑になっている。
処理は途中まで主成分分析のそれに近い。
つまり、まずは中心化したデータの分散共分散行列について固有値問題を解いて回転ベクトル を手に入れる。
次に、回転ベクトルの逆行列と分散共分散行列と回転行列の内積を計算して、これを
とおく。
続いて の逆行列の平方根と、回転行列と中心化したデータの内積を計算して
とおく。
この が白色化したデータを表す。
まあ、上の式だけを眺めていてもなんのこっちゃという感じなのでサンプルコードを以下に示す。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from sklearn import datasets from matplotlib import pyplot as plt def main(): iris = datasets.load_iris() X = iris.data[:, 2:] # データを中心化する (平均を引くことで平均を 0 にする) X_centerized = X - X.mean(axis=0) # 分散共分散行列を計算する Sigma = np.cov(X, rowvar=0) # 固有値問題を解いて固有値と固有ベクトル (回転行列) を得る _, S = np.linalg.eig(Sigma) # 回転行列の逆行列 S_inv = np.linalg.inv(S) # 対角行列 Lambda = S_inv.dot(Sigma).dot(S) # 対角成分だけ残す Lambda = (Lambda * np.identity(2)).transpose() # 各対角要素の平方根をとった行列の逆行列 Lambda_sqrt_inv = np.linalg.inv(np.sqrt(Lambda)) # 白色化する u = X_centerized.dot(S).dot(Lambda_sqrt_inv.T) # 白色化後の分散共分散行列 u_cov = np.cov(u, rowvar=0) print('白色化後の分散共分散行列: {cov}'.format(cov=u_cov)) # 同、平均 u_mu = u.mean(axis=0) print('白色化後の平均: {mu}'.format(mu=u_mu)) # 同、標準偏差 u_std = u.std(axis=0) print('白色化後の標準偏差: {std}'.format(std=u_std)) plt.scatter(X[:, 0], X[:, 1], label='before') plt.scatter(u[:, 0], u[:, 1], label='after') plt.ylim((-3, 3)) plt.xlim((-2, 8)) plt.xlabel('petal length') plt.ylabel('petal width') plt.plot([0, 0], [-3, 3], 'k--') plt.plot([-2, 8], [0, 0], 'k--') plt.grid(True) plt.legend() plt.show() if __name__ == '__main__': main()
上記をファイルに保存して実行してみる。
$ python whitening.py 白色化後の分散共分散行列: [[ 1.00000000e+00 -3.81499455e-16] [ -3.81499455e-16 1.00000000e+00]] 白色化後の平均: [ -1.36631447e-15 2.68192875e-15] 白色化後の標準偏差: [ 0.99666109 0.99666109]
出力内容から白色化後のデータは相関がなくなって平均が 0 になり標準偏差が 1 になることがわかった。
また、同時に次のような散布図が得られる。
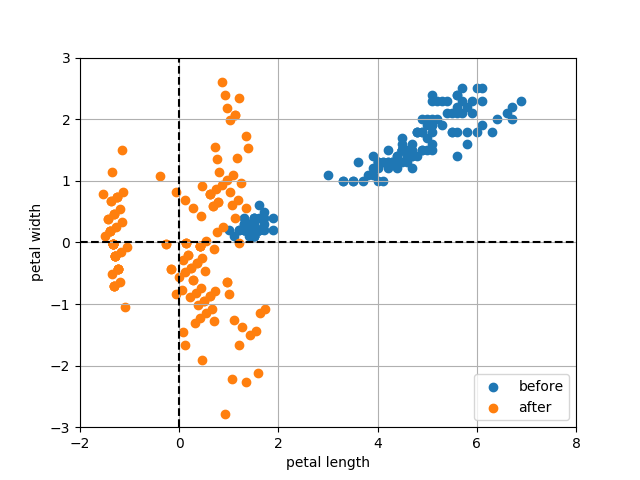
どの点がどの点に対応するのかも、もはやよく分からないほどだけど、これで良いようだ。
まとめ
今回はデータの前処理として無名数化と呼ばれる手法をいくつか試してみた。 無名数化というのは、データに含まれる次元の単位をなくす処理のことだった。
まずはじめに、標準化と呼ばれるデータの平均を 0 にして標準偏差を 1 にする手法を紹介した。 その次の無相関化では、データの各次元間の共分散 (相関) を 0 にできた。 そして、最後に紹介した白色化では共分散 (相関) を 0 にした上で平均を 0 標準偏差を 1 にできた。
参考文献

- 作者: 平井有三
- 出版社/メーカー: 森北出版
- 発売日: 2012/07/31
- メディア: 単行本(ソフトカバー)
- 購入: 1人 クリック: 7回
- この商品を含むブログ (4件) を見る

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログ (1件) を見る