Python: TrueSkill が収束する様子を眺めてみる

TrueSkill は 2 人以上のプレイヤーまたはチームが対戦して勝敗を決める競技において、プレイヤーの実力を数値にする手法のひとつ。 TrueSkill は Microsoft が開発して特許や商標を保持している。そのため、アルゴリズムを商用で利用するためには同社からライセンスを受ける必要がある。なんでも Xbox のゲームでプレイヤーの実力を数値化して、適正なマッチングをするために使われているらしい。同種のレーティングアルゴリズムとして有名なイロレーティング (Elo Rating) に比べると、次のようなメリットがある。

1 vs 1 以外の競技にも使える
レーティングの収束が早い
レーティングの不確実性が得られる

なお、今回のエントリは以下のレーティングアルゴリズムを TrueSkill にしたバージョンとなっている。

blog.amedama.jp

使った環境は次のとおり。

$ sw_vers
ProductName:        macOS
ProductVersion:     13.5
BuildVersion:       22G74
$ python -V             
Python 3.10.12
$ pip list | egrep -i "(matplotlib|trueskill|numpy)"
matplotlib      3.7.2
numpy           1.25.1
trueskill       0.4.5

下準備

$ pip install trueskill matplotlib

サンプルコード

これから示すサンプルコードは 2 つのフェーズに分かれている。

理論上のイロレーティングを与えたプレイヤーからモンテカルロ法で擬似的な対戦データを作成するフェーズ
作成した擬似的な対戦データから TrueSkill のレーティングの推移を計算して収束する様子を観察するフェーズ

まず 1. については、あらかじめ特定の値でイロレーティングを指定したプレイヤー同士をランダムに対戦させて、その勝率が疑似乱数を上回るかどうかで作成する。この点は、イロレーティングが理論上の対戦勝率を計算できる点を利用している。

そして 2. については、1. で作成した疑似データを使って、各プレイヤーが初期値の状態から TrueSkill のレーティングを更新していく。このとき、疑似データが十分にあれば、理論上のレーティングへと収束していくはずである。

疑似データは Alice, Bob, Charlie, David, Eve, Frank という名前をつけた 6 人のプレイヤーから生成する。 6 人のプレイヤーは各ラウンドでランダムにシャッフルされて 2 人ずつ対戦する。対戦した際の勝者は、前述したとおり事前に規定したイロレーティングと疑似乱数にもとづいて計算される。

以下にサンプルコードを示す。各プレイヤーは 200 刻みで理論上のイロレーティングを付与している。そして、500 回のラウンドを実施する。各ラウンドは 3 回の対戦が含まれるため、全体で 1,500 回の対戦が生じる。 TrueSkill の計算については、Python の trueskill パッケージを利用した。

import logging
import random

import numpy as np
from matplotlib import pyplot as plt
from trueskill import Rating
from trueskill import rate_1vs1


LOG = logging.getLogger(__name__)


class Player:
    """プレイヤーを表現したクラス"""

    def __init__(self, rating=1500):
        self.rating = rating

    def win_proba(self, other_player: "Player") -> float:
        """他のプレイヤーに勝利する確率を計算するメソッド"""
        return 1. / (10. ** ((other_player.rating - self.rating) / 400.) + 1.)


def simulated_match(player_a: Player, player_b: Player) -> bool:
    """モンテカルロ法でプレイヤー同士を対決させる

    :returns: シミュレーションで player_a が勝利したかを表す真偽値
    """
    player_a_win_ratio = player_a.win_proba(player_b)
    return random.random() < player_a_win_ratio


def main():
    # ログレベルを設定する
    logging.basicConfig(level=logging.INFO)

    # 乱数シードを固定する
    random.seed(42)

    # プレイヤーの理論上のレーティング
    ideal_players = {
        "Alice": Player(2000),
        "Bob": Player(1800),
        "Charlie": Player(1600),
        "David": Player(1400),
        "Eve": Player(1200),
        "Frank": Player(1000),
    }

    # モンテカルロ法で対戦履歴を生成する
    match_results = []
    for _ in range(500):
        # プレイヤーをシャッフルする
        shuffled_player_names = random.sample(
            list(ideal_players.keys()),
            len(ideal_players),
        )
        while len(shuffled_player_names) > 0:
            # シャッフルした結果から 1 vs 1 を取り出していく
            player_a_name, player_b_name = shuffled_player_names.pop(), shuffled_player_names.pop()
            player_a, player_b = ideal_players[player_a_name], ideal_players[player_b_name]
            # レーティングとランダムな値を元に対戦結果を求める
            win_player_name = player_a_name if simulated_match(player_a, player_b) else player_b_name
            match_results.append((player_a_name, player_b_name, win_player_name))
            # 対戦成績をログに出力する
            LOG.info(
                "match %s vs %s, winner: %s",
                player_a_name,
                player_b_name,
                win_player_name,
            )

    # プレイヤーのレーティング履歴
    simulated_players = {
        "Alice": [Rating()],
        "Bob": [Rating()],
        "Charlie": [Rating()],
        "David": [Rating()],
        "Eve": [Rating()],
        "Frank": [Rating()],
    }

    # 対戦成績を 1 件ずつ処理する
    for player_a_name, player_b_name, win_player_name in match_results:
        # 勝利プレイヤーと敗北プレイヤーの名前を取り出す
        winner_name = win_player_name
        loser_name = player_b_name if win_player_name == player_a_name else player_a_name

        # 履歴で最後 (最新) のレーティングを取り出す
        winner = simulated_players[winner_name][-1]
        loser = simulated_players[loser_name][-1]

        # 対戦成績を元にレーティングを更新する
        updated_winner, updated_loser = rate_1vs1(winner, loser)

        # 履歴の末尾に追加する
        simulated_players[winner_name].append(updated_winner)
        simulated_players[loser_name].append(updated_loser)

        # レーティングの更新をログに出力する
        LOG.info(
            "winner %s %.3f (%.2f) -> %.3f (%.2f), loser %s %.3f (%.2f) -> %.3f (%.2f)",
            winner_name,
            winner.mu,
            updated_winner.sigma,
            updated_winner.mu,
            updated_winner.sigma,
            loser_name,
            loser.mu,
            loser.sigma,
            updated_loser.mu,
            updated_loser.sigma,
        )

    # 最終的なレーティングをログに出力する
    for player_name, player_history in simulated_players.items():
        LOG.info(
            "player %s %.3f (%.2f)",
            player_name,
            player_history[-1].mu,
            player_history[-1].sigma,
        )

    # レーティングの推移を折れ線グラフで可視化する
    fig, ax = plt.subplots(1, 1)
    for player_name, player_history in simulated_players.items():
        # ミュー (推定されたレーティング) を折れ線グラフで図示する
        player_mu_history = np.array([player.mu for player in player_history])
        ax.plot(
            player_mu_history,
            label=player_name,
        )
        # シグマ (不確実性) を半透明の領域で折れ線の上下に図示する
        player_sigma_history = np.array([player.sigma for player in player_history])
        ax.fill_between(
            range(1, len(player_history) + 1),
            player_mu_history - player_sigma_history,
            player_mu_history + player_sigma_history,
            alpha=0.3,
        )
    ax.set_title(f"TrueSkill Rating History")
    ax.set_xlabel("Rounds")
    ax.set_ylabel("Rating")
    ax.grid()
    ax.legend()
    plt.show()


if __name__ == "__main__":
    main()

上記を実行しよう。すると、最初に擬似的な対戦成績がログとして出力される。その次に TrueSkill のレーティングが更新される様子がログとして出力される。最後に、最終的なレーティングを出力している。

$ python ts.py 
INFO:__main__:match David vs Bob, winner: Bob
INFO:__main__:match Charlie vs Eve, winner: Charlie
INFO:__main__:match Alice vs Frank, winner: Alice
...(省略)...
INFO:__main__:winner Bob 31.327 (0.95) -> 31.351 (0.95), loser David 22.064 (0.89) -> 22.043 (0.89)
INFO:__main__:winner Alice 36.249 (1.08) -> 36.279 (1.08), loser Charlie 26.857 (0.90) -> 26.835 (0.90)
INFO:__main__:winner Eve 18.549 (0.94) -> 18.623 (0.94), loser Frank 14.695 (1.03) -> 14.606 (1.03)
INFO:__main__:player Alice 36.279 (1.08)
INFO:__main__:player Bob 31.351 (0.95)
INFO:__main__:player Charlie 26.835 (0.90)
INFO:__main__:player David 22.043 (0.89)
INFO:__main__:player Eve 18.623 (0.94)
INFO:__main__:player Frank 14.606 (1.03)

上記でカッコ内の数値はレーティングの不確実さを表している。言いかえると、値が小さいほど、そのレーティングの数値を信頼できる。

また、実行が完了すると次のような折れ線グラフが得られる。これは、各プレイヤーのレーティングの推移を示している。網掛けの部分はレーティングの不確実性を表している。

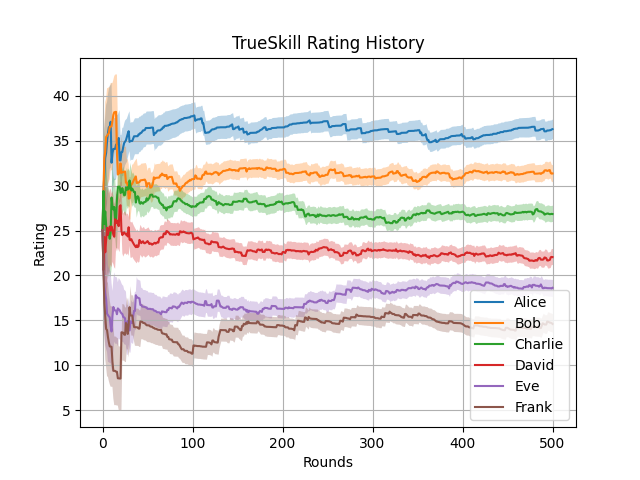
上記から 100 ラウンドほどで収束している様子が確認できる。これは、先のエントリで確認したイロレーティングが収束するラウンドよりも少ない。

なお、イロレーティングと TrueSkill ではデフォルトで使用される平均的なプレイヤーの数値が異なる。一般にイロレーティングでは 1500 を使う一方で、今回利用した TrueSkill の実装では 25 になっている。そのため擬似的な対戦データを生成するのに使った理論上のイロレーティングの数値と TrueSkill の数値が大きく異なっている。

両者を比較しやすいようにイロレーティングの数値を TrueSkill の数値に換算してみよう。まず、今回はプレイヤーのイロレーティングの理論値を次のようにした。

>>> import numpy as np
>>> elo_ratings = np.array([2000, 1800, 1600, 1400, 1200, 1000])

レーティングの数値から平均を引いて標準偏差で割ることで標準化する。これでレーティングは平均が 0 で標準偏差が 1 になる。

>>> normalized_ratings = (elo_ratings - elo_ratings.mean()) / elo_ratings.std()
>>> normalized_ratings
array([ 1.46385011,  0.87831007,  0.29277002, -0.29277002, -0.87831007,
       -1.46385011])

次に標準化した数値に TrueSkill で使われている標準偏差をかけて平均を足す。これで先ほどのイロレーティングの数値が TrueSkill の数値に換算できるはず。

>>> trueskill_ratings = normalized_ratings * 8.333333333333334 + 25
>>> trueskill_ratings
array([37.19875091, 32.31925055, 27.43975018, 22.56024982, 17.68074945,
       12.80124909])

先ほど実行した結果で、最終的に収束したレーティングの数値と比べると近いことが確認できる。

めでたしめでたし。