Python: scikit-learn で決定木 (Decision Tree) を試してみる

今回は機械学習アルゴリズムの一つである決定木を scikit-learn で試してみることにする。決定木は、その名の通り木構造のモデルとなっていて、分類問題ないし回帰問題を解くのに使える。また、決定木自体はランダムフォレストのような、より高度なアルゴリズムのベースとなっている。

使うときの API は scikit-learn が抽象化しているので、まずは軽く触ってみるところから始めよう。決定木がどんな構造を持ったモデルなのかは最後にグラフで示す。また、決定木自体は回帰問題にも使えるけど、今回は分類問題だけにフォーカスしている。

使った環境は次の通り。

$ sw_vers    
ProductName:    Mac OS X
ProductVersion: 10.12.4
BuildVersion:   16E195
$ python --version
Python 3.5.3

下準備

まずは、今回のサンプルコードを動かすのに必要な Python のパッケージをインストールしておく。

$ pip install scipy scikit-learn matplotlib

アイリスデータセットを分類してみる

まずは定番のアイリス (あやめ) データセットを決定木で分類してみることにする。といっても scikit-learn を使う限りは、分類器が違っても API は同じなので使用感は変わらない。

次のサンプルコードではアイリスデータセットに含まれる三種類の花の品種を決定木で分類している。モデルの汎化性能は LOO 法を使って計算した。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import LeaveOneOut
from sklearn.metrics import accuracy_score


def main():
    # アイリスデータセットを読み込む
    dataset = datasets.load_iris()

    # 教師データとラベルデータを取り出す
    features = dataset.data
    targets = dataset.target

    # 判定したラベルデータを入れるリスト
    predicted_labels = []
    # LOO 法で汎化性能を調べる
    loo = LeaveOneOut()
    for train, test in loo.split(features):
        # 学習に使うデータ
        train_data = features[train]
        target_data = targets[train]

        # モデルを学習させる
        clf = DecisionTreeClassifier()
        clf.fit(train_data, target_data)

        # テストに使うデータを正しく判定できるか
        predicted_label = clf.predict(features[test])
        predicted_labels.append(predicted_label)

    # テストデータでの正解率 (汎化性能) を出力する
    score = accuracy_score(targets, predicted_labels)
    print(score)


if __name__ == '__main__':
    main()

上記を実行すると、次のような結果が得られる。約 95.3% の汎化性能が得られた。ただし、決定木はどんな木構造になるかが毎回異なるので汎化性能も微妙に異なってくる。

0.953333333333

ハイパーパラメータを調整する

機械学習アルゴリズムで、人間が調整してやらなきゃいけないパラメータのことをハイパーパラメータという。決定木では、木構造の深さがモデルの複雑度を調整するためのハイパーパラメータになっている。深いものはより複雑で、浅いものはより単純なモデルになる。

次のサンプルコードは、決定木の深さを指定した数に制限した状態での汎化性能を示すものになっている。具体的な深さについては 1 ~ 20 を順番に試行している。ちなみに、指定できるのは「最大の深さ」なので、できあがる木構造がそれよりも浅いということは十分にありうる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import LeaveOneOut
from sklearn.metrics import accuracy_score


def main():
    dataset = datasets.load_iris()

    features = dataset.data
    targets = dataset.target

    # 調べる深さ
    MAX_DEPTH = 20
    depths = range(1, MAX_DEPTH)

    # 決定木の最大深度ごとに正解率を計算する
    accuracy_scores = []
    for depth in depths:

        predicted_labels = []
        loo = LeaveOneOut()
        for train, test in loo.split(features):
            train_data = features[train]
            target_data = targets[train]

            clf = DecisionTreeClassifier(max_depth=depth)
            clf.fit(train_data, target_data)

            predicted_label = clf.predict(features[test])
            predicted_labels.append(predicted_label)

        # 各深度での汎化性能を出力する
        score = accuracy_score(targets, predicted_labels)
        print('max depth={0}: {1}'.format(depth, score))

        accuracy_scores.append(score)

    # 最大深度ごとの正解率を折れ線グラフで可視化する
    X = list(depths)
    plt.plot(X, accuracy_scores)

    plt.xlabel('max depth')
    plt.ylabel('accuracy rate')
    plt.show()


if __name__ == '__main__':
    main()

上記の実行結果は次の通り。前述した通り決定木がどんな木構造になるかは毎回異なるので、これも毎回微妙に異なるはず。

max depth=1: 0.3333333333333333
max depth=2: 0.9533333333333334
max depth=3: 0.9466666666666667
max depth=4: 0.9466666666666667
max depth=5: 0.9466666666666667
max depth=6: 0.9466666666666667
max depth=7: 0.9466666666666667
max depth=8: 0.94
max depth=9: 0.9533333333333334
max depth=10: 0.94
max depth=11: 0.9533333333333334
max depth=12: 0.9466666666666667
max depth=13: 0.9466666666666667
max depth=14: 0.94
max depth=15: 0.94
max depth=16: 0.9466666666666667
max depth=17: 0.96
max depth=18: 0.9466666666666667
max depth=19: 0.9466666666666667

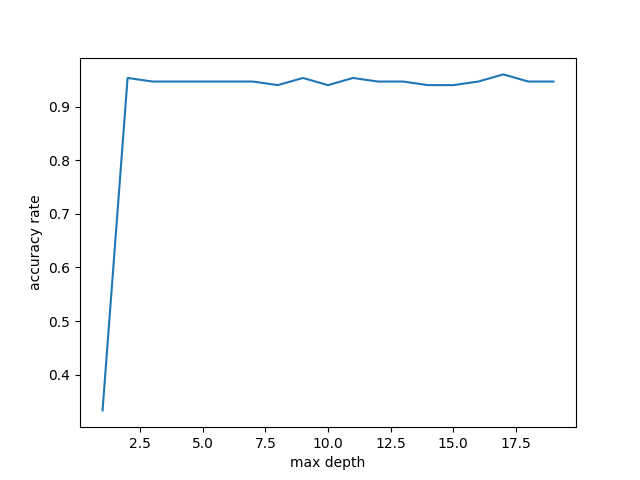
同時に、次のような折れ線グラフが得られる。どうやら、今回のケースでは最大の深さが 3 以上であれば、汎化性能はどれもそんなに変わらないようだ。 f:id:momijiame:20170425221114p:plain

どのように分類されているのか可視化してみる

先ほどは深さによって汎化性能がどのように変わってくるかを見てみた。今回扱うデータセットでは 3 以上あれば汎化性能にはさほど大きな影響がないらしいことが分かった。次は、木構造の深さ (つまりモデルの複雑度) によって分類のされ方がどのように変わるのかを見てみたい。

次のサンプルコードでは、二次元の散布図を元に分類される様子を見るために教師データを二次元に絞っている。具体的には、データセットの教師データの中から「Petal length」と「Petal width」だけを取り出して使っている。その上で、それぞれを x 軸と y 軸にプロットした。また、同時にどの点がどの品種として分類されているかを背景に色付けしている。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier


def main():
    dataset = datasets.load_iris()

    features = dataset.data
    targets = dataset.target

    # Petal length と Petal width だけを特徴量として使う (二次元で図示したいので)
    petal_features = features[:, 2:]

    # 決定木の最大深度は制限しない
    clf = DecisionTreeClassifier()
    clf.fit(petal_features, targets)

    # 教師データの取りうる範囲 +-1 を計算する
    train_x_min = petal_features[:, 0].min() - 1
    train_y_min = petal_features[:, 1].min() - 1
    train_x_max = petal_features[:, 0].max() + 1
    train_y_max = petal_features[:, 1].max() + 1

    # 教師データの取りうる範囲でメッシュ状の座標を作る
    grid_interval = 0.2
    xx, yy = np.meshgrid(
        np.arange(train_x_min, train_x_max, grid_interval),
        np.arange(train_y_min, train_y_max, grid_interval),
    )

    # メッシュの座標を学習したモデルで判定させる
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    # 各点の判定結果をグラフに描画する
    plt.contourf(xx, yy, Z.reshape(xx.shape), cmap=plt.cm.bone)

    # 教師データもプロットしておく
    for c in np.unique(targets):
        plt.scatter(petal_features[targets == c, 0],
                    petal_features[targets == c, 1])

    feature_names = dataset.feature_names
    plt.xlabel(feature_names[2])
    plt.ylabel(feature_names[3])
    plt.show()


if __name__ == '__main__':
    main()

このモデルについては木構造の深さを制限していない。

上記を実行すると、次のような散布図が得られる。

f:id:momijiame:20170425221614p:plain

次は、上記のサンプルコードに木構造の深さの制限を入れてみよう。とりあえず最大の深さを 3 までに制限してみる。前述した通り、こうしても汎化性能自体には大きな影響はないようだった。分類のされ方には変化が出てくるだろうか？

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier


def main():
    dataset = datasets.load_iris()

    features = dataset.data
    targets = dataset.target

    petal_features = features[:, 2:]

    # 決定木の深さを 3 までに制限する
    clf = DecisionTreeClassifier(max_depth=3)
    clf.fit(petal_features, targets)

    train_x_min = petal_features[:, 0].min() - 1
    train_y_min = petal_features[:, 1].min() - 1
    train_x_max = petal_features[:, 0].max() + 1
    train_y_max = petal_features[:, 1].max() + 1

    grid_interval = 0.2
    xx, yy = np.meshgrid(
        np.arange(train_x_min, train_x_max, grid_interval),
        np.arange(train_y_min, train_y_max, grid_interval),
    )
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    plt.contourf(xx, yy, Z.reshape(xx.shape), cmap=plt.cm.bone)

    for c in np.unique(targets):
        plt.scatter(petal_features[targets == c, 0],
                    petal_features[targets == c, 1])

    feature_names = dataset.feature_names
    plt.xlabel(feature_names[2])
    plt.ylabel(feature_names[3])
    plt.show()


if __name__ == '__main__':
    main()

上記を実行すると、次のような散布図が得られる。

f:id:momijiame:20170425222036p:plain

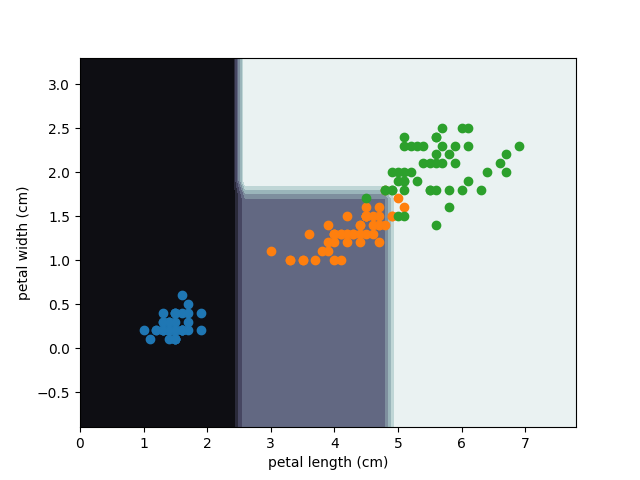
先ほどの例と比べてみよう。オレンジ色の品種が緑色の品種のところに食い込んでいるところが、このケースでは正しく認識されなくなっている。モデルがより単純になったと考えられるだろう。

木構造を可視化してみる

scikit-learn には決定木の構造を DOT 言語で出力する機能がある。その機能を使って木構造を可視化してみることにしよう。

まずは DOT 言語を処理するために Graphviz をインストールする。

$ brew install graphviz

そして、次のように学習させたモデルから DecisionTreeClassifier#export_graphviz() メソッドで DOT 言語で書かれたファイルを出力させる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree


def main():
    dataset = datasets.load_iris()

    features = dataset.data
    targets = dataset.target

    # Petal length と Petal width だけを特徴量として使う
    petal_features = features[:, 2:]

    # モデルを学習させる
    clf = DecisionTreeClassifier(max_depth=3)
    clf.fit(petal_features, targets)

    # DOT 言語のフォーマットで決定木の形を出力する
    with open('iris-dtree.dot', mode='w') as f:
        tree.export_graphviz(clf, out_file=f)


if __name__ == '__main__':
    main()

これを Graphviz で画像データに変換する。

$ dot -T png iris-dtree.dot -o iris-dtree.png

すると、次のようなグラフが得られる。

f:id:momijiame:20170425223006p:plain

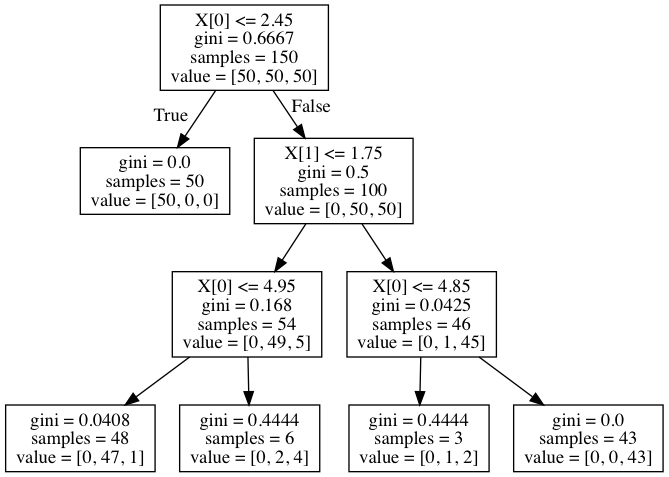
グラフでは、葉ノード以外が分類をするための分岐になっている。これは、ようするに木構造が深くなるに従ってだんだんと対象を絞り込んでいっていることを意味する。例えば、最初の分岐では x 軸が 2.45 未満のところで分岐している。そして、左側の葉ノードは青色の品種が全て集まっていることが分かる。

まとめ

今回は決定木を scikit-learn で試してみた
決定木はランダムフォレストのようなアルゴリズムのベースとなっている
決定木のモデルの複雑さは木構造の深さで制御する
木構造の深さが浅くなるほど分類のされ方も単純になった

はじめてのパターン認識

作者: 平井有三
出版社/メーカー: 森北出版
発売日: 2012/07/31
メディア: 単行本（ソフトカバー）
購入: 1人クリック: 7回
この商品を含むブログ (3件) を見る

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ

作者: もみじあめ
発売日: 2016/03/12
メディア: Kindle版
この商品を含むブログ (1件) を見る

CUBE SUGAR CONTAINER

技術系のこと書きます。

Python: scikit-learn で決定木 (Decision Tree) を試してみる

下準備

アイリスデータセットを分類してみる

ハイパーパラメータを調整する

どのように分類されているのか可視化してみる

木構造を可視化してみる

まとめ