今回は、データセットのある次元の値から別の次元の値を予測する方法の一つとして、最小二乗法というやり方で回帰直線を求めてみる。 とはいえ、いきなり最小二乗法や回帰直線といわれても何が何やらという感じなので、最初はその説明からしていく。
回帰
まず、ある次元の値から別の次元の値を予測するというのは具体的にどういうことだろうか。 例えば、賃貸の部屋の広さと家賃の値段に相関関係があるとしよう。 つまり、広い部屋はそれだけ家賃も高いということで、これは直感に反していない。 だとすれば、部屋の広さと家賃の値段の関係が含まれたデータセットがあるとき、部屋の広さから家賃の値段を予測できるはずだ。
統計や機械学習の世界では、このような問題のジャンルに「教師あり学習」の「回帰」という名前がついている。 ただし、ある次元の値から別の次元の値を予測する問題がすべて回帰と呼ばれるわけではない。 なぜかというと、その次元に含まれるデータの種類によって、やることが異なるため。
データの種類には、大きく分けて二つある。 まず、男性や女性、あるいは好きな食べ物といった、いくつかの種類からひとつを選ぶようなものは質的データという。 それに対し、年齢や一日の摂取カロリーなど、値が連続性を持ったものは量的データという。
ある次元から別の次元を予測するとき、予測する対象が質的データなら「分類」で、量的データなら「回帰」になる。 そして、予測の元ネタになるデータのことを説明変数、予測する値のことを応答変数と呼ぶ。 このとき、説明変数がひとつなら単回帰、複数なら重回帰と呼ばれる。
以上から、今回このエントリでやってみるのは単回帰になる。 回帰直線というのは、説明変数と応答変数の関係を次の一次式で表した直線のこと。
このとき、 が説明変数で
は応答変数を表している。
と
は切片と傾きに対応していて、これは回帰係数と呼ばれている。
最小二乗法
最小二乗法というのは、教師データに最もフィットする回帰係数を見つける手法のことをいう。
最小二乗法では、次に示す を最小化するようになっている。
ここで
は
の予測値を表している。
予測値にはハットの記号をつける慣例になっているため。
この
のことを残差という。
ようするに、これは真の値と予測値との差のこと。
より具体的には、この残差を自乗した合計値が最も小さくなる回帰係数を見つけるのが目的になる。
これを残差平方和という。 自乗しているのは符号をすべてプラスにするため。
これは を展開すると、こうなる。
これを最小にする回帰係数を得る手法を最小二乗法という
具体的な手順
先ほどの式は と
で偏微分して、それが 0 に等しいとすると連立一次方程式に直すことができる、らしい。
が、そこに至るまでの過程はひとまず飛ばして、先人の知恵だけ享受することにする。
まず、必要なのは次の回帰直線を表した一次式。
この中で、まずは は、次の式で得られる。
ここで、 は
と
の共分散を表している。
つまり、こう。
共分散や相関関係については、前回のエントリに詳しく書いたので見てもらいたい。
また、 は
の分散を表している。
つまり、こう。
は
の平均値を表すので、こうだね。
そして、次に は、次のようにして得られる。
と同様に、
は
の平均値を表している。
数式がずらずら並んでなんのこっちゃという感じになってきたので、まとめると…
という回帰直線の一次式に含まれる回帰係数 と
は、それぞれ
と
という式で得られる、ということ。
実際に計算してみよう
では、上記を Python のプログラムで実際に計算して上手くいくか試してみよう。
サンプルプログラムでは matplotlib を使ってグラフを描いているので、まずはインストールしておく。
$ pip install matplotlib
次が肝心のサンプルプログラム。 中で最小二乗法を使って回帰直線を得ている。
#!/usr/bin/env python # -*- coding: utf-8 -*- from __future__ import division from matplotlib import pyplot as plt import numpy as np def main(): # データ点数は 100 にする N = 100 # 0 ~ 10 (-5 ~ +5) の範囲で、ランダムに値を散らばらせる R = 10 x = np.arange(N) # y = 50 + x の直線に (-5 ~ +5) でランダム性をもたせる y = np.arange(N) + np.random.rand(N) * R - R // 2 + 50 # 平均値と標準偏差 xmu, xsigma2 = x.mean(), x.var() # 平均値 ymu = y.mean() # 共分散 sxy = np.sum(x * y) / N - xmu * ymu # 回帰係数ベータ beta = sxy / xsigma2 # 回帰係数アルファ alpha = ymu - beta * xmu # 得られた回帰直線の一次式 print('y = {0} + {1}x'.format(alpha, beta)) # グラフに回帰直線をひく lsm = np.array([alpha + beta * xi for xi in x]) plt.plot(x, lsm, color='r') # 元データもプロットする plt.scatter(x, y) # グラフを表示する plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show() if __name__ == '__main__': main()
これを lsm.py という名前をつけて実行してみる。
$ python lsm.py y = 49.52693410299069 + 0.9984255719901004x
データにはランダム性を持たせているため、微妙に異なるものの、ほぼ の一次式が得られている!
また、可視化したグラフは次のようになった。
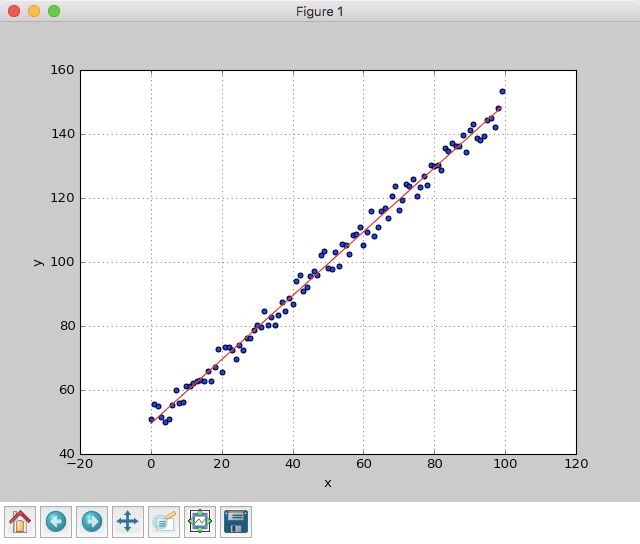
データに沿って、ちゃんと回帰直線がひけていることが分かる。
まとめ
- データセットのある次元から別の次元を予測するのに、回帰という問題のジャンルがある
- 予測するデータの種類によって問題の呼び方は異なる
- 質的データなら「分類」になる
- 量的データなら「回帰」になる
- 予測の元ネタを説明変数、予測する値のことを応答変数という
- 説明変数がひとつの次元なら単回帰、ふたつ以上なら重回帰という
- 回帰のやり方のひとつに最小二乗法という手法がある
- 最小二乗法では残差平方和を最小化する
- 予測値と真の値との差を残差という
- 残差の自乗をすべて足したものが残差平方和
- 説明変数と応答変数の関係を一次式で表した直線を回帰直線という
- 回帰直線のパラメータとなる
と
を回帰係数という
- 回帰直線のパラメータとなる
おまけ
回帰係数の は式変形すると別の求め方もできる。
これには、回帰係数 と
と
の標準偏差を使う。
回帰係数は、次のように求める。
ここで、 は共分散なので、次のように求める。
と
は標準偏差なので、こう。
と
は平均値なので、こう。
これを、先ほどのプログラムに適用してみる。
#!/usr/bin/env python # -*- coding: utf-8 -*- from __future__ import division from matplotlib import pyplot as plt import numpy as np def main(): N = 100 R = 10 x = np.arange(N) y = np.arange(N) + np.random.rand(N) * R - R // 2 + 50 xmu, xsigma = x.mean(), x.std() ymu, ysigma = y.mean(), x.std() sxy = np.sum(x * y) / N - xmu * ymu rxy = sxy / (xsigma * ysigma) beta = rxy * (ysigma / xsigma) alpha = ymu - beta * xmu print('y = {0} + {1}x'.format(alpha, beta)) lsm = np.array([alpha + beta * xi for xi in x]) plt.plot(x, lsm, color='r') plt.scatter(x, y) plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show() if __name__ == '__main__': main()
実行結果は次の通り。
$ python lsm2.py y = 50.359765922390736 + 0.9931534165033539x
グラフもこのように。

どちらでも、大丈夫だね。

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログを見る









