以前、このブログで一変数の関数から勾配法で最小値を探す記事を書いた。
このときは題材として という一変数の関数を扱った。
今回は、これを多変数の関数に拡張してみることにする。
ちなみに、この多変数というのは機械学習における多次元と同じ意味を持っている。
つまり、これができると多次元のデータセットで損失関数の出力から最小値を探すことができることを意味している。
使った環境は次の通り。
$ sw_vers ProductName: Mac OS X ProductVersion: 10.11.6 BuildVersion: 15G1108 $ python --version Python 3.5.2
下準備
まずは、前回と同じように可視化に使う matplotlib と、数値計算用のライブラリである numpy をインストールしておこう。
$ pip install matplotlib numpy
多変数の関数を解析的に偏微分する
今回題材として扱う関数は にする。
勾配法では最初に関数を微分する必要があった。 これは、関数が多変数になったときも変わらない。 ただし、多変数になると名前だけは偏微分と呼ばれるようになる。 また、変数が複数あるので、それぞれの関数について微分することになる。
試しに、題材とする関数を について解析的に偏微分してみよう。
このとき、微分する対象ではない変数
は固定値と捉える。
そのため、結果は
となる。
次のサンプルコードでは のときの
を計算している。
とはいえ、上記の内容から結果は
とすぐに分かる。
#!/usr/bin/env python # -*- coding: utf-8 -*- def f(x0, x1): """偏微分したい関数: f(x) = x_0^2 + x_1^2""" return x0 ** 2 + x1 ** 2 def df_x0(x0, x1): """関数 f の解析的な x0 についての偏微分: f'(x) = 2x_0""" return 2 * x0 # x_1 は固定値と捉えて微分することで消滅しており登場しない def main(): grad = df_x0(3.0, 4.0) # ぶっちゃけ x_1 は影響を与えないので何を使っても良い print('解析的な x0 についての偏微分: {0}'.format(grad)) if __name__ == '__main__': main()
実行結果は次の通り。 まあ、当たり前だね。
解析的な x0 についての偏微分: 6.0
多変数の関数から数値解法で偏微分の近似値を得る
先ほどの例では人が数式を見て解析的に偏微分したけど、これだと機械学習アルゴリズムには適用が難しい。 近似値で良いから、先ほどの偏微分をコンピュータにやらせたい。 そこで、今度は前回のブログでも扱った中央差分を元にした数値微分を適用してみることにしよう。
次のサンプルコードを見てほしい。
ここでは、先ほどと同じように のときの
を計算している。
ポイントとしては、偏微分というのは微分に使わない変数を固定値として扱うところだ。
なので
を
4.0 に固定した関数 f_x0 を定義している。
そして、その関数を前回のブログ記事にも登場した数値微分の関数 numerical_diff で微分している。
#!/usr/bin/env python # -*- coding: utf-8 -*- def f(x0, x1): """偏微分したい関数: f(x) = x0^2 + x1^2""" return x0 ** 2 + x1 ** 2 def f_x0(x0): """関数 f を x0 について偏微分するために x1 を固定値にした関数""" return f(x0, 4.0) def numerical_diff(f, x): """中央差分を元に数値微分する関数""" h = 1e-4 return (f(x + h) - f(x - h)) / (2 * h) def main(): grad = numerical_diff(f_x0, 3.0) print('数値微分を使った x0 についての偏微分: {0}'.format(grad)) if __name__ == '__main__': main()
上記を実行してみよう。
数値微分を使った x0 についての偏微分: 6.00000000000378
おお!解析的な偏微分で得られた値とほとんど同じ値 (近似値) が得られている!
NumPy を使って汎用的にしてみる
先ほどのサンプルコードでは偏微分をするために、微分に関係しない変数を固定値にした関数を新たに用意していた。
しかし、これを毎回やるのは大変なので、今度は数値微分の関数 numerical_diffを偏微分用に拡張してみよう。
次のサンプルコードでは、偏微分する関数 f の引数を変更している。
具体的には、これまで別々の引数としていた と
を NumPy の配列で渡すことにしている。
また、偏微分に拡張した関数
numerical_diff には引数 i を追加している。
これは、引数 x のうち何番目の要素で偏微分するかを表すインデックスになっている。
例えば なら
について偏微分することを意味している。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np def f(x): """偏微分したい関数: f(x) = x0^2 + x1^2""" return x[0] ** 2 + x[1] ** 2 def numerical_diff(f, x, i): """中央差分を元に数値微分する関数 (偏微分) :param function f: 偏微分する関数 :param numpy.ndarray x: 偏微分する引数 :param int i: 偏微分する変数のインデックス """ # 丸め誤差で無視されない程度に小さな値を用意する h = 1e-4 # 偏微分する変数のインデックスにだけ上記の値を入れる h_vec = np.zeros_like(x) h_vec[i] = h # 数値微分を使って偏微分する return (f(x + h_vec) - f(x - h_vec)) / (2 * h) def main(): args = [3.0, 4.0] # 偏微分に使う引数 grad = numerical_diff(f, args, 0) # 0 番目の要素 (x0) について偏微分する print('数値微分を使った x0 についての偏微分: {0}'.format(grad)) if __name__ == '__main__': main()
ポイントとしては偏微分する要素にだけ丸め誤差で無視されない程度に小さな値を加えて数値微分している点だ。
上記を実行してみよう。
数値微分を使った x0 についての偏微分: 6.00000000000378
先ほどと同じように上手く偏微分できていることが分かる。
偏微分を元に勾配を計算する
多変数の関数において、各変数について偏微分して得られた値をベクトルにまとめたものを勾配と呼ぶ。 次は、この勾配を計算してみよう。 とはいえ、ある変数について偏微分するやり方は先ほどの例で分かったので、あとはそれを繰り返すだけ。
次のサンプルコードでは numerical_gradient という関数で購買を計算している。
ポイントは特に無くて、各変数について淡々と偏微分するだけ。
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np def f(x): """偏微分したい関数: f(x) = x0^2 + x1^2""" return x[0] ** 2 + x[1] ** 2 def numerical_diff(f, x, i): """中央差分を元に数値微分する関数 (偏微分) :param function f: 偏微分する関数 :param numpy.ndarray x: 偏微分する引数 :param int i: 偏微分する変数のインデックス """ # 丸め誤差で無視されない程度に小さな値を用意する h = 1e-4 # 偏微分する変数のインデックスにだけ上記の値を入れる h_vec = np.zeros_like(x) h_vec[i] = h # 数値微分を使って偏微分する return (f(x + h_vec) - f(x - h_vec)) / (2 * h) def numerical_gradient(f, x): """勾配を計算する関数 勾配というのは、全ての変数について偏微分した結果をベクトルとしてまとめたものを言う。 """ # 勾配を入れるベクトルをゼロで初期化する grad = np.zeros_like(x) for i, _ in enumerate(x): # i 番目の変数で偏微分する grad[i] = numerical_diff(f, x, i) # 計算した勾配を返す return grad def main(): grad = numerical_gradient(f, np.array([3.0, 4.0])) print('勾配: {0}'.format(grad)) if __name__ == '__main__': main()
実行すると のときの勾配が得られる。
勾配: [ 6. 8.]
題材となる関数を可視化してみる
さて、先ほどのサンプルコードで勾配を計算することができた。 とはいえ、何のために勾配を計算したのかよく分からないかもしれないので、ここで補足しておく。 先ほど計算した勾配には、それぞれの変数について偏微分したときの傾きが入っている。 これはつまり、各次元ごとのどちらに進めば値が小さくなるかという情報だ。
上記の説明だけでは分かりづらいかもしれないので、より原点に立ち返った説明もしてみよう。
例えば という三つの軸を持った三次元の空間をイメージしてほしい。
通常であれば変数の名前は
になるけど、ここではあえて今回使った変数の名前にしている。
まず
と
が関数の入力で
が出力だとしよう。
縦と横が
と
に対応していて高さが
ということになる。
今回の問題は高さ
が最も低くなる位置を
と
の平面の中から探したいということだ。
試しに、今回題材とする関数 を上記のように三次元で捉えて可視化してみることにしよう。
#!/usr/bin/env python # -*- coding: utf-8 -*- from mpl_toolkits.mplot3d import Axes3D from matplotlib import pyplot as plt import numpy as np def main(): x0 = np.arange(-2, 2, 0.1) x1 = np.arange(-2, 2, 0.1) X0, X1 = np.meshgrid(x0, x1) Y = X0 ** 2 + X1 ** 2 fig = plt.figure() ax = Axes3D(fig) ax.plot_wireframe(X0, X1, Y) plt.show() if __name__ == '__main__': main()
上記を実行すると、次のようなグラフが得られる。
 上記より、最小値は
上記より、最小値は ということが分かる。
偏微分を元にした勾配の計算というのは、上記のグラフでいえば各点における傾きを という、それぞれの軸ごとに計算するという意味になる。
勾配法への組み込み
ここで、前回も扱った勾配法の数式を多変数に拡張して示す。
上記で現在の位置を としたとき、より最小値に近づいたものが
になる。
は学習率と呼ばれるもので、どれくらいの勢いで最小値に近づいていくかを表している。
そして
は
を
について偏微分した関数になる。
上記は、扱う変数が増えて多変数 (多次元) になったとしてもアルゴリズムの基本は全く変わらない。
単に、各次元ごとにそれぞれで勾配法を実行するだけだ。
次のサンプルコードでは初期位置を として、学習率
0.01 ステップ数 50 回で勾配法を実行している。
#!/usr/bin/env python # -*- coding: utf-8 -*- from matplotlib import pyplot as plt import numpy as np def f(x): """偏微分したい関数: f(x) = x0^2 + x1^2""" return x[0] ** 2 + x[1] ** 2 def numerical_diff(f, x, i): """中央差分を元に数値微分する関数 (偏微分) :param function f: 偏微分する関数 :param numpy.ndarray x: 偏微分する引数 :param int i: 偏微分する変数のインデックス """ # 丸め誤差で無視されない程度に小さな値を用意する h = 1e-4 # 偏微分する変数のインデックスにだけ上記の値を入れる h_vec = np.zeros_like(x) h_vec[i] = h # 数値微分を使って偏微分する return (f(x + h_vec) - f(x - h_vec)) / (2 * h) def numerical_gradient(f, x): """勾配を計算する関数 勾配というのは、全ての変数について偏微分した結果をベクトルとしてまとめたものを言う。 """ # 勾配を入れるベクトルをゼロで初期化する grad = np.zeros_like(x) for i, _ in enumerate(x): # i 番目の変数で偏微分する grad[i] = numerical_diff(f, x, i) # 計算した勾配を返す return grad def gradient_descent(f, initial_position, learning_rate=0.1, steps=50): """勾配法で最小値を求める関数 :param function f: 最小値を見つけたい関数 :param numpy.ndarray initial_position: 関数の初期位置 :param float learning_rate: 学習率 :param int steps: 学習回数 """ # 現在地を示すカーソル x = initial_position # 学習を繰り返す for _ in range(steps): # 現在地の勾配 (どちらにどれだけ進むべきか) を得る grad = numerical_gradient(f, x) # 勾配を元にして現在地を移動する x -= learning_rate * grad # 最終的な位置を返す return x def main(): # 勾配法を使って関数 f() の最小値を探す (初期位置は 1, 2) min_pos = gradient_descent(f, [1, 2]) print('勾配法が見つけた最小値: {0}'.format(min_pos)) if __name__ == '__main__': main()
上記を実行した結果は次の通り。
勾配法が見つけた最小値: [ 1.78405962e-05 3.56811923e-05]
最小値である に、どちらの次元についても近づけていることが分かる。
最小値に収束していく様子を可視化してみる
先ほどの結果から、最小値に収束させることができることは分かった。 次は、どのように収束していっているのかをグラフで可視化してみよう。
次のサンプルコードでは各ステップごとの と
の位置を折れ線グラフで示している。
#!/usr/bin/env python # -*- coding: utf-8 -*- from matplotlib import pyplot as plt import numpy as np def f(x): """偏微分したい関数: f(x) = x0^2 + x1^2""" return x[0] ** 2 + x[1] ** 2 def numerical_diff(f, x, i): """中央差分を元に数値微分する関数 (偏微分) :param function f: 偏微分する関数 :param numpy.ndarray x: 偏微分する引数 :param int i: 偏微分する変数のインデックス """ # 丸め誤差で無視されない程度に小さな値を用意する h = 1e-4 # 偏微分する変数のインデックスにだけ上記の値を入れる h_vec = np.zeros_like(x) h_vec[i] = h # 数値微分を使って偏微分する return (f(x + h_vec) - f(x - h_vec)) / (2 * h) def numerical_gradient(f, x): """勾配を計算する関数 勾配というのは、全ての変数について偏微分した結果をベクトルとしてまとめたものを言う。 """ # 勾配を入れるベクトルをゼロで初期化する grad = np.zeros_like(x) for i, _ in enumerate(x): # i 番目の変数で偏微分する grad[i] = numerical_diff(f, x, i) # 計算した勾配を返す return grad def gradient_descent(f, initial_position, learning_rate=0.1): """勾配法で最小値を求める関数 :param function f: 最小値を見つけたい関数 :param numpy.ndarray initial_position: 関数の初期位置 :param float learning_rate: 学習率 """ # 現在地を示すカーソル x = initial_position # 学習を繰り返す while True: # 現在地の勾配 (どちらにどれだけ進むべきか) を得る grad = numerical_gradient(f, x) # 勾配を元にして現在地を移動する x -= learning_rate * grad # 現在の位置を返す yield np.copy(x) def main(): g = gradient_descent(f, [1, 2]) x = range(50) y = np.array([next(g) for _ in x]) plt.plot(x, y[:, 0], label='f_x0(x)') plt.plot(x, y[:, 1], label='f_x1(x)') plt.legend() plt.show() if __name__ == '__main__': main()
上記の実行結果は次の通り。
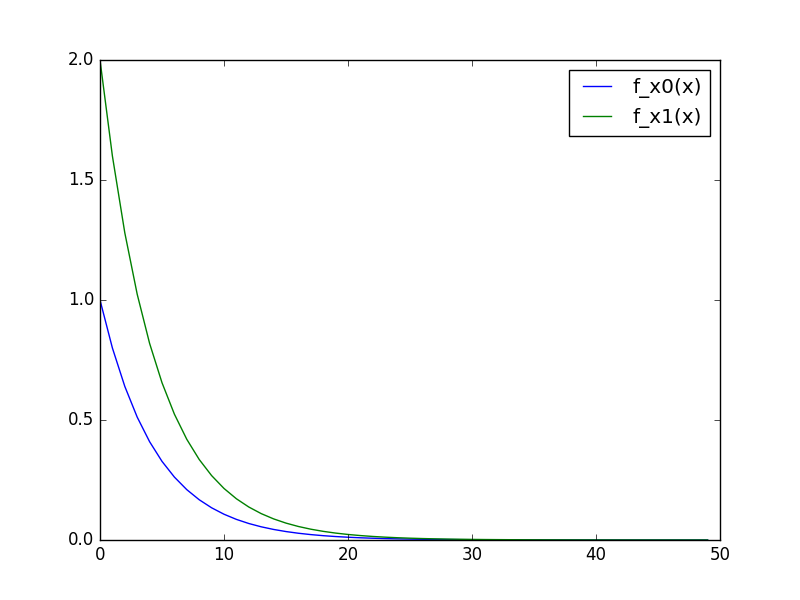 それぞれの軸で最小値に収束していく様子が見て取れる。
それぞれの軸で最小値に収束していく様子が見て取れる。
まとめ
- 勾配法は多変数の関数でも使える
- ただし傾きを得るときの計算が偏微分になる
- 偏微分は解析的に計算する必要はなく数値解法での近似値が使える
- 各変数について偏微分した結果のベクトルを勾配という
- 勾配を元に各次元ごとに最小値を探すことができる
参考文献

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
- 作者: 斎藤康毅
- 出版社/メーカー: オライリージャパン
- 発売日: 2016/09/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (6件) を見る

スマートPythonプログラミング: Pythonのより良い書き方を学ぶ
- 作者: もみじあめ
- 発売日: 2016/03/12
- メディア: Kindle版
- この商品を含むブログを見る