Python: 勾配法で関数の最小値を探す

勾配法はニューラルネットワークなどの機械学習アルゴリズムの中で、学習するときに使われているアルゴリズム。このアルゴリズムを使うと、与えられた関数の最小値 (または最大値) を探すことができる。例えば教師データと現在の出力の誤差を計算する損失関数を与えれば、その最小値を探すことで教師データに出力を近づけることができる。ただし、真の最小値 (または最大値) が見つかることが保証されているわけではなく、局所的な最適解に陥る恐れはある。

今回は Python を使って単純な勾配法を実装してみることにする。使った環境は次の通り。

$ sw_vers 
ProductName:    Mac OS X
ProductVersion: 10.11.6
BuildVersion:   15G1108
$ python --version
Python 3.5.2

パッケージのインストール

まずは可視化のための matplotlib と、数値計算系をするならこれがないとお話にならない numpy をインストールしておく。

$ pip install matplotlib numpy

題材にする関数

ひとまず、今回は $f(x) = x^{2}$ な関数を題材にしよう。この関数の最小値を勾配法を使って探してみることにする。

まずは最小値を求めたい関数をグラフに図示してみることにする。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
from matplotlib import pyplot as plt


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def main():
    x = np.arange(-2, 2, 0.1)

    y = f(x)
    plt.plot(x, y, label='f(x)')

    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

上記のプログラムを実行すると、次のようなグラフが得られる。 f:id:momijiame:20161210155342p:plain

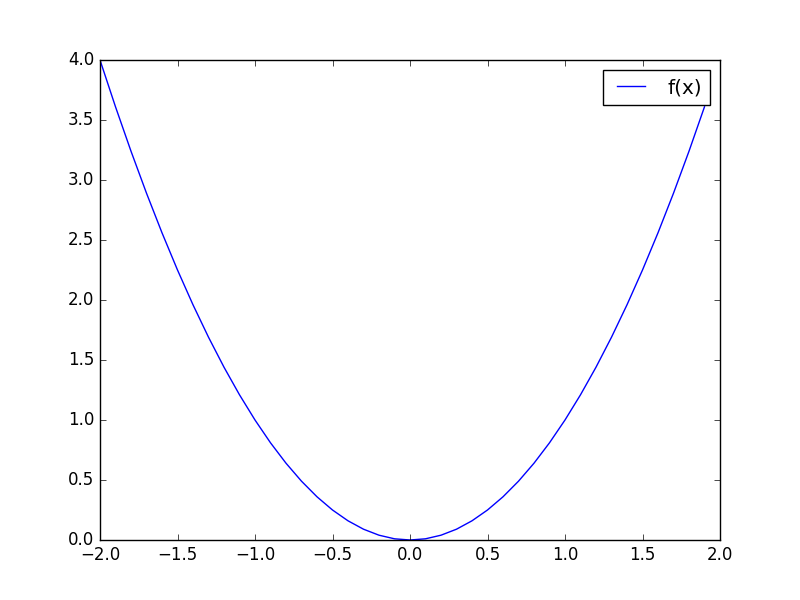
まあ、どう見ても最小値は $f(0)$ のときなことが分かる。

一階導関数を求める

先ほどはグラフから最小値をあっさりと判断できたけど、それは可視化した上で人間が判断しているため。コンピュータに最小値を探させるには、別の方法が必要になる。それに、今回は変数がひとつだけなので良いものの、みっつ以上に増えれば可視化も難しくなる。

そこで登場するのが今回の勾配法なわけだけど、これにはまず最小値を求めたい関数を微分する必要がある。ちなみに、このやり方であれば人間の判断は必要なくなって、変数が増えたときにも偏微分で対応できる。

ではまず、先ほどの関数 $f(x) = x^{2}$ を微分したものをグラフにしてみよう。これは $f'(x) = 2x$ ということが分かる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
from matplotlib import pyplot as plt


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def df(x):
    """最小値を求めたい関数の一階導関数"""
    return 2 * x


def main():
    x = np.arange(-2, 2, 0.1)

    y = f(x)
    plt.plot(x, y, label='f(x)')

    y_dash = df(x)
    plt.plot(x, y_dash, label='f\'(x)')

    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

最終的には微分までコンピュータにやらせるけど、ここではあえて人間が微分している。

上記を実行すると、次のようなグラフが得られる。 f:id:momijiame:20161210160243p:plain

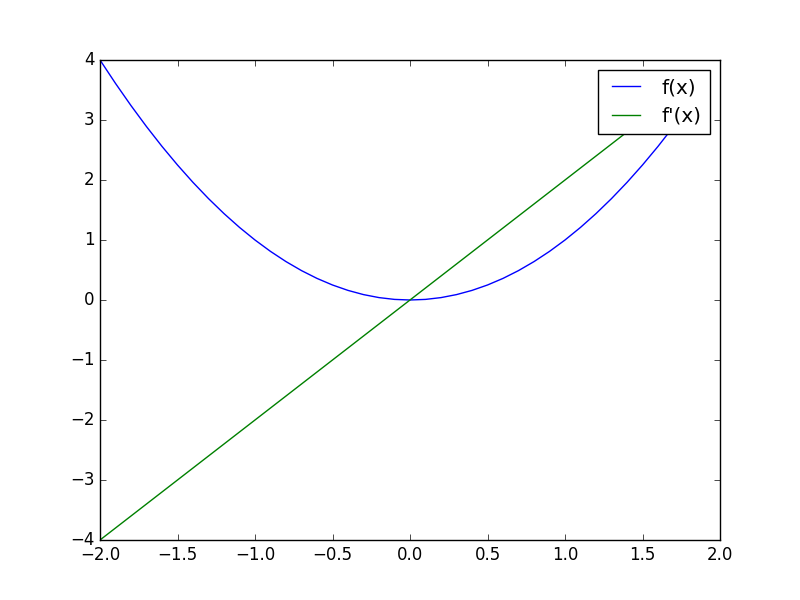
青色の線が最小値を求めたい関数で、緑色の線が一階導関数になっている。最小値である $f(0)$ を境にして、一階導関数の出力がプラスとマイナスに切り替わっていることが見て取れる。

f:id:momijiame:20161210161205p:plain

勾配法では、この最小値を境にして一階導関数のプラスとマイナスが切り替わるところが重要になる。

一階導関数の符号を反転してみると？

先ほどの一階導関数をそのままプロットしたグラフでは、最小値よりも大きい範囲ではプラスに、小さい範囲ではマイナスになっていた。これの符号を反転してみると、どうなるだろうか？

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
from matplotlib import pyplot as plt


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def df(x):
    """最小値を求めたい関数の一階導関数"""
    return 2 * x


def main():
    x = np.arange(-2, 2, 0.1)

    y = f(x)
    plt.plot(x, y, label='f(x)')

    y_dash = df(x)
    # 一階導関数の符号を反転させる
    plt.plot(x, -y_dash, label='-f\'(x)')

    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

上記を実行すると、次のようなグラフが得られる。 (グラフでは凡例にマイナス符号を付けるのを忘れていた)

f:id:momijiame:20161210161748p:plain

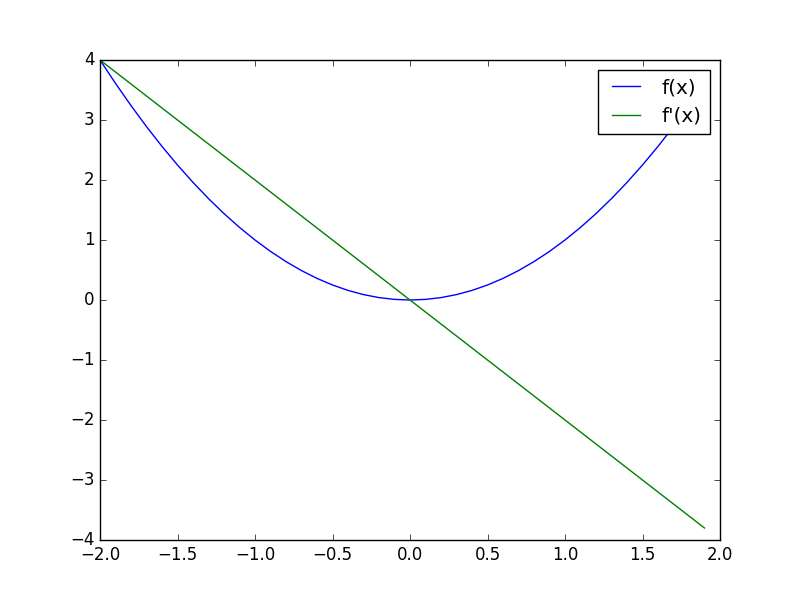
今度のグラフでは一階導関数が最小値を境にして大きい範囲ではマイナス、小さい範囲ではプラスになっている。すると、符号を反転した一階導関数の出力は、最小値に近づけるために必要な移動方向と一致することが分かる。

f:id:momijiame:20161210162141p:plain

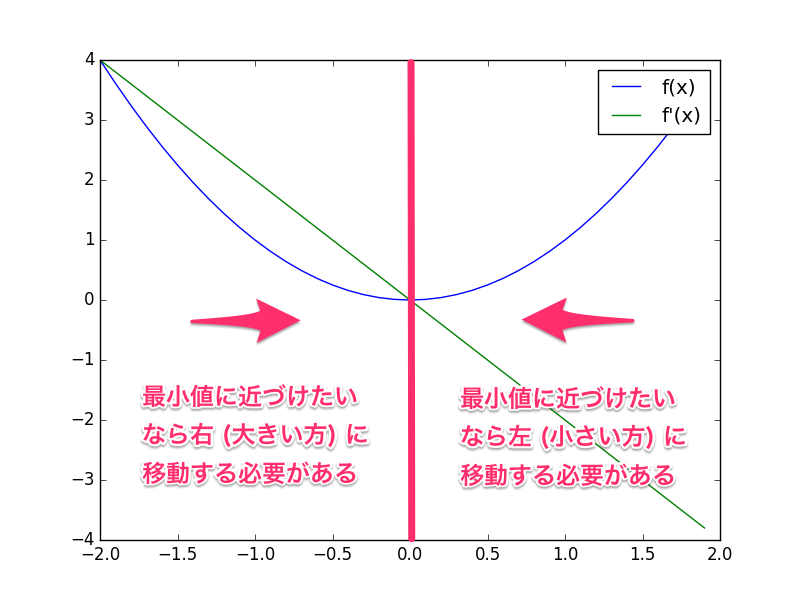
つまり、最小値は符号を反転した一階導関数を出力が指し示す方向にあるということになる。あとは、その指し示す方向を頼りに徐々に移動していけば、いつかは最小値にたどり着ける。

とはいえ、もちろんたどり着いた先が局所的な最適解で、実際の最小値が別にある可能性はある。これはようするに、関数の出力がぐねぐねしていて、ところどころに凹みがあると、そこにハマってしまうということ。

勾配法

ここで勾配法のアルゴリズムを数式で書いてみよう。

$x_{i + 1} = x_i - \eta f'(x_i)$

上記で現在の位置を $x_i$ としたとき、より最小値に近づいたものが $x_{i + 1}$ になる。 $\eta$ は学習率と呼ばれるもので、どれくらいの勢いで最小値に近づいていくかを表している。そして $f'(x_i)$ は最小値を探したい関数の一階導関数になっている。

勾配法では、上記の作業を複数回繰り返すことで最小値を探す。次のサンプルコードでは gradient_descent() という関数で勾配法を実装している。 learning_rate が学習率 $\eta$ に対応していて steps は上記の工程を何回繰り返すかを表す。初期値は 1 に設定した上で最小値をそこから探していく。

#!/usr/bin/env python
# -*- coding: utf-8 -*-


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def df(x):
    """最小値を求めたい関数の一階導関数"""
    return 2 * x


def gradient_descent(df, initial, learning_rate=0.1, steps=50):
    """一階導関数から勾配法で最小値を求める関数"""
    # 現在地を示すカーソル
    x = initial

    # 所定の回数を繰り返す
    for _ in range(steps):
        # 現在地の勾配 (どちらにどれだけ進むべきか) を得る
        grad = df(x)
        # 勾配を元にして現在地を移動する
        x -= learning_rate * grad

    # 最終的な位置を返す
    return x


def main():
    print(gradient_descent(df, 1))


if __name__ == '__main__':
    main()

上記を実行すると次のような出力が得られる。

1.4272476927059604e-05

値は $1.4272476927059604 * 10^{-5}$ なので 0 に近いことが分かる。

勾配法の learning_rate や steps はハイパーパラメータと呼ばれていて人間が適切に選ぶ必要がある。これは大きくても小さくても上手くいかない。例えば learning_rate が大きすぎれば移動する量が大きすぎていつまでも収束せず、小さすぎれば最小値になかなか近づかない。また steps は大きすぎれば計算量が大きくなりすぎるし、小さすぎれば最小値に近づくまでに終了してしまう。

最小値に収束していく様子を可視化してみる

先ほどは最小値に収束した結果だけを出力にしたけど、次は収束していく様子を可視化してみる。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from matplotlib import pyplot as plt


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def df(x):
    """最小値を求めたい関数の一階導関数"""
    return 2 * x


def gradient_descent(df, initial, learning_rate=0.1):
    """一階導関数から勾配法で最小値を求める関数"""
    # 現在地を示すカーソル
    x = initial

    while True:
        # 現在地の勾配 (どちらにどれだけ進むべきか) を得る
        grad = df(x)
        # 勾配を元にして現在地を移動する
        x -= learning_rate * grad

        yield x


def main():
    g = gradient_descent(df, 1)

    x = range(50)
    y = [next(g) for _ in x]

    plt.plot(x, y)
    plt.show()


if __name__ == '__main__':
    main()

上記を実行すると、次のようなグラフが得られる。

f:id:momijiame:20161210165835p:plain

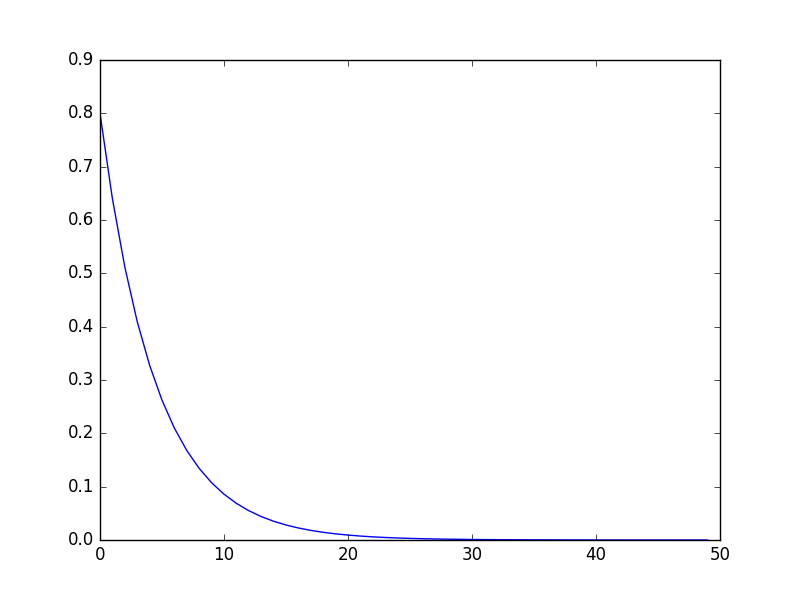
工程を繰り返すごとに、初期値である 1 付近から、徐々に最小値である 0 に近づいていくことが見て取れる。

微分をコンピュータにやらせる

ここまでで勾配法を使って最小値を探すことができることは分かった。しかし、先ほどの例ではまだ人間が最小値を探したい関数を微分していた。これをどうにかしないことには機械学習には使えない。

そこで、まずは微分の定義から見直してみよう。

$\begin{eqnarray}f'(x) = \frac{ df(x) }{ dx } = \lim_{ h \to 0 } \frac{ f(x + h) - f(x) }{ h }\end{eqnarray}$

上記は $f(x)$ に、限りなくゼロに近づけた小さな値 $h$ を加えたときの変化量 (傾き) を得る、という意味になっている。ただし、これをそのまま実世界のコンピュータに適用することはできない。

まず、限りなくゼロに近づけた値は IEEE754 の小数を実装したコンピュータでは正しく扱うことができない。まず、あまりにも小さい値は丸め誤差で無視されてしまう。

>>> 1e-100
1e-100
>>> 1.0 + 1e-100
1.0

そのため、定義どおりに限りなくゼロに近づけたような値ではなく、丸め誤差で無視されない程度に小さな値を使うことになる。

さらに、限りなくゼロに近づけた値が使えないために生じる問題がある。丸め誤差で無視されない程度に小さな値 $h$ を $f(x)$ に加えて傾きを求めるとしよう。すると、実際に傾きを求めたい場所 $x$ からは $h$ だけ位置ズレてしまう。

そこで、上記の問題を解決するために中央差分というものを使って変化量を求める。これは、求めたい場所 $x$ の前後 $\pm h$ の差分を使って傾きを求めるというもの。これなら傾きを求める場所のズレは前後 $\pm h$ で打ち消されて $x$ そのものになる。

試しに、上記で説明した中央差分を使った微分で一階導関数を求めてみよう。次のサンプルコードでは numerical_diff() という関数で中央差分を元にした微分を実装している。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
from matplotlib import pyplot as plt


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def numerical_diff(f, x):
    """中央差分を元に数値微分する関数"""
    h = 1e-4
    return (f(x + h) - f(x - h)) / (2 * h)


def main():
    x = np.arange(-2, 2, 0.1)

    y = f(x)
    plt.plot(x, y, label='f(x)')

    y_dash = numerical_diff(f, x)
    plt.plot(x, y_dash, label='f\'(x)')

    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

ちなみに、先ほどのように人間が数式から手計算で微分することを解析的な微分と呼ぶ。それに対し、上記サンプルコードのようなコンピュータを使った近似的な微分を数値微分という。

上記を実行すると次のグラフが得られる。

f:id:momijiame:20161210173103p:plain

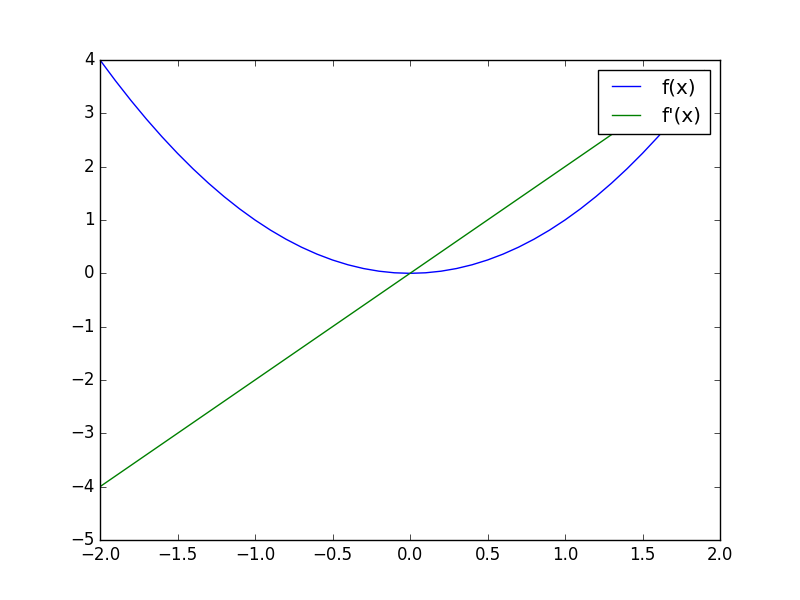
グラフで見る限り解析的な微分したときと同じ結果が得られている。

数値微分を勾配法に組み込んでみる

今回の記事の最終形態として、先ほどの勾配法に数値微分を組み込んでみよう。

#!/usr/bin/env python
# -*- coding: utf-8 -*-


def f(x):
    """最小値を求めたい関数"""
    return x ** 2


def numerical_diff(f, x):
    """中央差分を元に数値微分する関数"""
    h = 1e-4
    return (f(x + h) - f(x - h)) / (2 * h)


def gradient_descent(f, initial, learning_rate=0.1, steps=50):
    """一階導関数から勾配法で最小値を求める関数"""
    # 現在地を示すカーソル
    x = initial

    # 所定の回数を繰り返す
    for _ in range(steps):
        # 現在地の勾配 (どちらにどれだけ進むべきか) を得る
        grad = numerical_diff(f, x)
        # 勾配を元にして現在地を移動する
        x -= learning_rate * grad

    # 最終的な位置を返す
    return x


def main():
    print(gradient_descent(f, 1))


if __name__ == '__main__':
    main()